题目内容
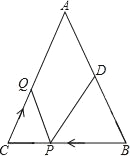
【题目】如图,在△ABC中,∠BAC=90°,AB=AC.点D从点B出发沿射线BC移动,以AD为边在AB的右侧作△ADE,且∠DAE=90°,AD=AE.连接CE.
(1)如图1,若点D在BC边上,则∠BCE=______度;
(2)如图2,若点D在BC的延长线上运动.
①∠BCE的度数是否发生变化?请说明理由;
②若BC=6,CD=2,求△ADE的面积.

【答案】(1)90;(2)①不发生变化.②17
【解析】
(1)根据等腰直角三角形性质证∠BAD=∠CAE,再证△ACE≌△ABD(SAS);∠ACE=∠ABD=45°;∠BCE=∠BCA+∠ACE=45°+45°;(2)①运用(1)方法可得角度不发生变化;②过点A作AF⊥BC,垂足为F,在等腰直角三角形△ABF和△ACF中,求出FD,BD,根据△ACE≌△ABD,求出CE=BD=8,根据S△ADE=![]() 可得.
可得.
解:(1)∵AB=AC,∠BAC=90°
∴∠ABC=∠ACB=45°,
∵∠BAC=∠DAE=90°
∴∠BAC+∠DAC=∠DAE+∠DAC
∴∠BAD=∠CAE,
在△ACE和△ABD中
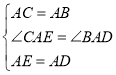
∴△ACE≌△ABD(SAS)
∴∠ACE=∠ABD=45°
∴∠BCE=∠BCA+∠ACE=45°+45°=90°
(2)①不发生变化.
∵AB=AC,∠BAC=90°
∴∠ABC=∠ACB=45°,
∵∠BAC=∠DAE=90°
∴∠BAC+∠DAC=∠DAE+∠DAC
∴∠BAD=∠CAE,
在△ACE和△ABD中
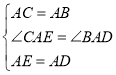
∴△ACE≌△ABD(SAS)
∴∠ACE=∠ABD=45°
∴∠BCE=∠BCA+∠ACE=45°+45°=90°
∴∠BCE的度数不变,为90°
②如图,过点A作AF⊥BC,垂足为F
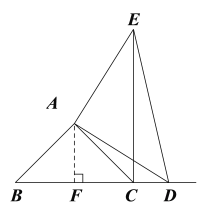
∴△ABF和△ACF为等腰直角三角形
∴AF=![]() BC=3
BC=3
∴FD=5
∵BC=6,CD=2
∴BD=8
∵△ACE≌△ABD
∴CE=BD=8,
∴S△ADE=![]()
=![]()
=17

 阅读快车系列答案
阅读快车系列答案【题目】在不透明的袋子中有黑棋子10枚和白棋子若干(它们除颜色外都相同),现随机从中摸出10枚记下颜色后放回,这样连续做了10次,记录了如下的数据:
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
黑棋数 | 1 | 3 | 0 | 2 | 3 | 4 | 2 | 1 | 1 | 3 |
根据以上数据,估算袋中的白棋子数量为( )
A. 60枚 B. 50枚 C. 40枚 D. 30枚