题目内容
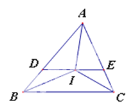
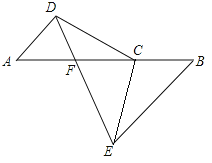
【题目】△ABC是一块直角三角形纸片,∠ACB=90°,将该三角形纸片折叠,使点A与点C重合,DE为折痕.

(1)线段AE和BE有怎样的数量关系?写出你的结论并进行证明.
结论: .
证明:
(2)直角三角形斜边的中线和斜边有怎样的数量关系?写出你的结论(不证明).
结论: .
【答案】(1)答案见解析;(2)答案见解析.
【解析】
(1)由折叠的性质可知∠A=∠ACE,然后利用等角的余角相等得出∠ECB=∠B,从而得到结论;(2)直角三角形斜边中线等于斜边的一半.
解:(1)AE=BE,证明如下:
由折叠性质可知:AE=CE, ∠A=∠ACE
∵∠ACB=90°
∴![]()
∴![]()
∴CE=BE
∴AE=BE
(2)如图:

在矩形ABCD中,根据矩形性质可知:![]() ,AO=CO=BO=DO=
,AO=CO=BO=DO=![]()
∴在Rt△ABC中,BO是斜边AC的中线且等于AC的
因此,直角三角形斜边中线等于斜边的一半.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目