题目内容
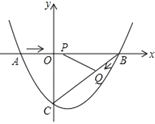
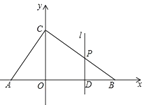
【题目】如图,在平面直角坐标系中,![]() 的斜边在
的斜边在![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上
轴上![]() ,
,![]() 、
、![]() 的长分别是一元二次方程
的长分别是一元二次方程![]() 的两个根,且
的两个根,且![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)![]() 是线段
是线段![]() 上的一个动点(点
上的一个动点(点![]() 不与点
不与点![]() ,
,![]() 重合),过点
重合),过点![]() 的直线
的直线![]() 与
与![]() 轴平行,直线
轴平行,直线![]() 交边
交边![]() 或边
或边![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长为
的长为![]() ,求
,求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)在(2)的条件下,当![]() 时,请你直接写出点P的坐标.
时,请你直接写出点P的坐标.
【答案】(1)![]() ;(2)
;(2)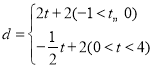 ;(3)
;(3)![]() ,
,![]() 或
或![]()
【解析】
(1)由一元二次方程可求得![]() 、
、![]() 的长,利用
的长,利用![]() 可求得
可求得![]() 的长,则可求得
的长,则可求得![]() 点坐标;
点坐标;
(2)由![]() 、
、![]() 、
、![]() 的坐标可分别求得直线
的坐标可分别求得直线![]() 、
、![]() 的解析式,当点
的解析式,当点![]() 在线段
在线段![]() 上时,则点
上时,则点![]() 在直线
在直线![]() 上,则可表示出
上,则可表示出![]() 点坐标,从而可表示出
点坐标,从而可表示出![]() 的长;当点
的长;当点![]() 在线段
在线段![]() 上时,则点
上时,则点![]() 在直线
在直线![]() 上,可表示出点
上,可表示出点![]() 的坐标,从而可表示出
的坐标,从而可表示出![]() 的长,即可求得
的长,即可求得![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)在(2)中所求的函数关系式中分别令![]() ,分别求得相应的
,分别求得相应的![]() 的值,即可求得
的值,即可求得![]() 点坐标.
点坐标.
解:(1)解方程![]() 可得
可得![]() 或
或![]() ,
,
![]() 、
、![]() 的长分别是一元二次方程
的长分别是一元二次方程![]() 的两个根,且
的两个根,且![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,且
,且![]() ,
,
![]() ,
,
![]()
![]() ,即
,即![]() ,解得
,解得![]() ,
,
![]() ;
;
(2)由(1)可知![]() ,
,![]() ,
,![]() ,
,
设直线![]() 解析式为
解析式为![]() ,
,
![]()
![]() ,解得
,解得![]() ,
,
![]() 直线
直线![]() 解析式为
解析式为![]() ,
,
同理可求得直线![]() 解析式为
解析式为![]() ,
,
当点![]() 在线段
在线段![]() 上时,即
上时,即![]() 时,则点
时,则点![]() 在直线
在直线![]() 上,
上,
![]() 点坐标为
点坐标为![]() ,
,
![]() ;
;
当点![]() 在线段
在线段![]() 上时,即
上时,即![]() 时,则点
时,则点![]() 在直线
在直线![]() 上,
上,
![]() 点坐标为
点坐标为![]() ,
,
![]() ;
;
综上可知![]() 关于
关于![]() 的函数关系式为
的函数关系式为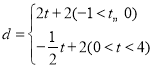 ;
;
(3)在![]() 中,令
中,令![]() ,可得
,可得![]() ,解得
,解得![]() ,
,
![]() ,
,![]() ;
;
在![]() 中,令
中,令![]() ,可得
,可得![]() ,解得
,解得![]() ,
,
![]() ;
;
综上可知当![]() 时,
时,![]() 点坐标为
点坐标为![]() ,
,![]() 或
或![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】甲、乙两店销售同一种蔬菜种子.在甲店,不论一次购买数量是多少,价格均为4.5元![]() .在乙店价格为5元
.在乙店价格为5元![]() ,如果一次购买2kg以上的种子,超出2kg部分的种子价格打8折.设小明在同一个店一次购买种子的数量为
,如果一次购买2kg以上的种子,超出2kg部分的种子价格打8折.设小明在同一个店一次购买种子的数量为![]() (
(![]() ).
).
(1)根据题意填表:
一次购买数量∕ | 1.5 | 2 | 3.5 | 6 | … |
在甲店花费∕元 | 6.75 | 15.75 | … | ||
在乙店花费∕元 | 7.5 | 16 | … |
(2)设在甲店花费![]() 元,在乙店花费
元,在乙店花费![]() 元,分别求
元,分别求![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)根据题意填空:
① 若小明在甲店和在乙店一次购买种子的数量相同,且花费相同,则他在同一个店一次购买种子的数量为 ![]() ;
;
② 若小明在同一个店一次购买种子的数量为3kg,则他在甲、乙两个店中的 店购买花费;
③ 若小明在同一个店一次购买种子花费了45元,则他在甲、乙两个店中的 店购买数量多.