ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ≈ΉΈοœΏyΘΫax2+bx+3Θ®aΓΌ0Θ©Ψ≠ΙΐΒψA(1Θ§0)ΚΆΒψB(3Θ§0)Θ§”κy÷αΫΜ”ΎΒψCΘ°
Θ®1Θ©«σ¥Υ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
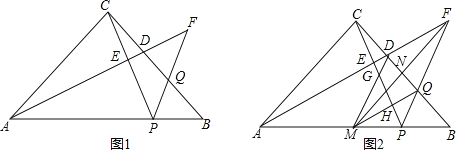
Θ®2Θ©»τΒψP «÷±œΏBCœ¬ΖΫΒΡ≈ΉΈοœΏ…œ“ΜΕ·ΒψΘ®≤ΜΒψBΘ§C÷ΊΚœΘ©Θ§ΙΐΒψPΉςy÷αΒΡΤΫ––œΏΫΜ÷±œΏBC”ΎΒψDΘ§…ηΒψPΒΡΚαΉχ±ξΈΣmΘ°
ΔΌ”ΟΚ§mΒΡ¥ζ ΐ Ϋ±μ ΨœΏΕΈPDΒΡ≥ΛΘ°
ΔΎΝ§Ϋ”PBΘ§PCΘ§«σΓςPBCΒΡΟφΜΐΉν¥σ ±ΒψPΒΡΉχ±ξΘ°
Θ®3Θ©…η≈ΉΈοœΏΒΡΕ‘≥Τ÷α”κBCΫΜ”ΎΒψEΘ§ΒψM «≈ΉΈοœΏΒΡΕ‘≥Τ÷α…œ“ΜΒψΘ§NΈΣy÷α…œ“ΜΒψΘ§ «Ζώ¥φ‘Ύ’β―υΒΡΒψMΚΆΒψNΘ§ ΙΒΟ“‘ΒψCΓΔEΓΔMΓΔNΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «Νβ–ΈΘΩ»γΙϊ¥φ‘ΎΘ§«κ÷±Ϋ”–¥≥ωΒψMΒΡΉχ±ξΘΜ»γΙϊ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°

ΓΨ¥πΑΗΓΩΘ®1Θ©yΘΫx2©¹4x+3ΘΜΘ®2Θ©ΔΌ©¹m2+3mΘ§ΔΎ(![]() Θ§©¹
Θ§©¹![]() )ΘΜΘ®3Θ©¥φ‘ΎΘ§ΒψMΒΡΉχ±ξΈΣ(2Θ§3)Θ§( 2Θ§1©¹2
)ΘΜΘ®3Θ©¥φ‘ΎΘ§ΒψMΒΡΉχ±ξΈΣ(2Θ§3)Θ§( 2Θ§1©¹2![]() )Μρ(2Θ§1+2
)Μρ(2Θ§1+2![]() )
)
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨί“―÷Σ≈ΉΈοœΏy=ax2+bx+3Θ®aΓΌ0Θ©Ψ≠ΙΐΒψAΘ®1Θ§0Θ©ΚΆΒψBΘ®3Θ§0Θ©¥ζ»κΦ¥Ω…«σΫβΘΜ
Θ®2Θ©ΔΌœ»»ΖΕ®÷±œΏBCΫβΈω ΫΘ§ΗυΨίΙΐΒψPΉςy÷αΒΡΤΫ––œΏΫΜ÷±œΏBC”ΎΒψDΘ§Φ¥Ω…”ΟΚ§mΒΡ¥χ…œ ι±μ Ψ≥ωPΚΆDΒΡΉχ±ξΫχΕχ«σΫβΘΜ
ΔΎ”ΟΚ§mΒΡ¥ζ ΐ Ϋ±μ Ψ≥ωΓςPBCΒΡΟφΜΐΘ§Ω…ΒΟS «ΙΊ”ΎmΒΡΕΰ¥ΈΚ· ΐΘ§Φ¥Ω…«σΫβΘΜ
Θ®3Θ©ΗυΨίΘ®1Θ©÷–ΥυΒΟΕΰ¥ΈΚ· ΐΆΦœσΚΆΕ‘≥Τ÷αœ»ΒΟΒψEΒΡΉχ±ξΦ¥Ω…–¥≥ωΒψ»ΐΗωΈΜ÷ΟΒΡΒψMΒΡΉχ±ξΘ°
ΫβΘΚΘ®1Θ©ΓΏ≈ΉΈοœΏyΘΫax2+bx+3Θ®aΓΌ0Θ©Ψ≠ΙΐΒψAΘ®1Θ§0Θ©ΚΆΒψBΘ®3Θ§0Θ©Θ§”κy÷αΫΜ”ΎΒψCΘ§
Γύ![]() Θ§
Θ§
ΫβΒΟΘΚ![]() ΘΜ
ΘΜ
Γύ≈ΉΈοœΏΫβΈω ΫΈΣΘΚyΘΫx2©¹4x+3ΘΜ
Θ®2Θ©»γΆΦΘΚ
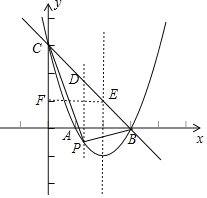
ΔΌ…ηPΘ®mΘ§m2©¹4m+3Θ©Θ§
ΫΪΒψBΘ®3Θ§0Θ©ΓΔCΘ®0Θ§3Θ©¥ζ»κΒΟ÷±œΏBCΫβΈω ΫΈΣyBCΘΫ©¹x+3Θ°
ΓΏΙΐΒψPΉςy÷αΒΡΤΫ––œΏΫΜ÷±œΏBC”ΎΒψDΘ§
ΓύDΘ®mΘ§©¹m+3Θ©Θ§
ΓύPDΘΫΘ®©¹m+3Θ©©¹Θ®m2©¹4m+3Θ©ΘΫ©¹m2+3mΘ°
¥πΘΚ”ΟΚ§mΒΡ¥ζ ΐ Ϋ±μ ΨœΏΕΈPDΒΡ≥ΛΈΣ©¹m2+3mΘ°
ΔΎSΓςPBCΘΫSΓςCPD+SΓςBPD
ΘΫ![]() OBPDΘΫ©¹
OBPDΘΫ©¹![]() m2+
m2+![]() m
m
ΘΫ©¹![]() Θ®m©¹
Θ®m©¹![]() Θ©2+
Θ©2+![]() Θ°
Θ°
ΓύΒ±mΘΫ![]() ±Θ§S”–Ήν¥σ÷ΒΘ°
±Θ§S”–Ήν¥σ÷ΒΘ°
Β±mΘΫ![]() ±Θ§m2©¹4m+3ΘΫ©¹
±Θ§m2©¹4m+3ΘΫ©¹![]() Θ°
Θ°
ΓύPΘ®![]() Θ§©¹
Θ§©¹![]() Θ©Θ°
Θ©Θ°
¥πΘΚΓςPBCΒΡΟφΜΐΉν¥σ ±ΒψPΒΡΉχ±ξΈΣΘ®![]() Θ§©¹
Θ§©¹![]() Θ©Θ°
Θ©Θ°
Θ®3Θ©¥φ‘Ύ’β―υΒΡΒψMΚΆΒψNΘ§ ΙΒΟ“‘ΒψCΓΔEΓΔMΓΔNΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «Νβ–ΈΘ°
ΗυΨίΧβ“βΘ§ΒψEΘ®2Θ§1Θ©Θ§
ΓύEFΘΫCFΘΫ2Θ§
ΓύECΘΫ![]() Θ§
Θ§
ΗυΨίΝβ–ΈΒΡΥΡΧθ±ΏœύΒ»Θ§
ΓύMEΘΫECΘΫ![]() Θ§
Θ§
ΓύMΘ®2Θ§1©¹![]() Θ©ΜρΘ®2Θ§1+
Θ©ΜρΘ®2Θ§1+![]() Θ©
Θ©
Β±EMΘΫEFΘΫ2 ±Θ§MΘ®2Θ§3Θ©
ΓύΒψMΒΡΉχ±ξΈΣM1Θ®2Θ§3Θ©Θ§M2Θ®2Θ§1©¹2![]() Θ©Θ§M3Θ®2Θ§1+2
Θ©Θ§M3Θ®2Θ§1+2![]() Θ©Θ°
Θ©Θ°