题目内容
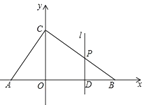
【题目】如图,![]() 是
是![]() 的直径,且
的直径,且![]() ,点
,点![]() 为
为![]() 外一点,且
外一点,且![]() ,
,![]() 分别切
分别切![]() 于点
于点![]() 、
、![]() 两点.
两点.![]() 与
与![]() 的延长线交于点
的延长线交于点![]() .
.
(1)求证:![]() ;
;
(2)填空
①当![]() ________时,四边形
________时,四边形![]() 是正方形.
是正方形.
②当![]() _________时,
_________时,![]() 为等边三角形.
为等边三角形.
【答案】(1)证明见解析;(2)6,![]() .
.
【解析】
(1)根据切线的性质及切线长定理可得MA⊥OA,MC⊥OC,MC=MA,然后根据等边对等角及等角的余角相等求出∠DCM=∠D,证得DM=MC即可得出结论;
(2)①根据正方形的判定定理可知当CM=OA=6时,四边形AOCM是正方形;
②根据等边三角形的性质可得∠D=60°,进而求出∠AOM=30°,然后解直角三角形求出AM即可解决问题.
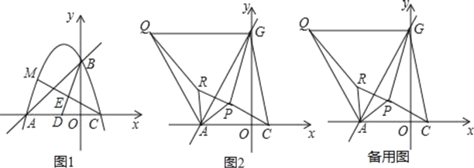
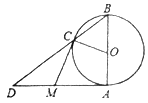
解:(1)如图1,连接OM,
∵MA,MC分别切⊙O于点A、C,
∴MA⊥OA,MC⊥OC,MC=MA,
∴∠DCM+∠OCB=90°,∠D+∠B=90°,
∵OC=OB,
∴∠OCB=∠B,
∴∠DCM=∠D,
∴DM=MC,
∴DM=MA;
(2)①如图2,当CM=6时,四边形AOCM是正方形;
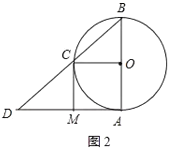
∵AB=12,
∴OA=OC=6,
又∵CM=AM=6,即AO=CO=AM=CM=6,
∴四边形AOCM是菱形,
又∵∠DAB=90°,
∴四边形AOCM是正方形;
②连接OM,如图3,
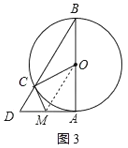
∵△DCM是等边三角形,
∴∠D=60°,
∵∠DAB=90°,
∴∠B=30°,
∴∠AOC=2∠B=60°,
∵AB=12,MA,MC分别切⊙O于点A、C,
∴OA=6,∠AOM=30°,
∴tan∠AOM=tan30°=![]() ,
,
∴AM=![]() ,
,
∴CM=AM=![]() ,
,
即当CM=![]() 时,△CDM为等边三角形.
时,△CDM为等边三角形.

练习册系列答案
相关题目