题目内容
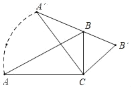
【题目】如图1是自动卸货汽车卸货时的状态图，图2是其示意图．汽车的车厢采用液压机构、车厢的支撑顶杆BC的底部支撑点B在水平线AD的下方，AB与水平线AD之间的夹角是5°，卸货时，车厢与水平线AD成60°，此时AB与支撑顶杆BC的夹角为45°，若AC＝2米，求BC的长度．（结果保留一位小数）
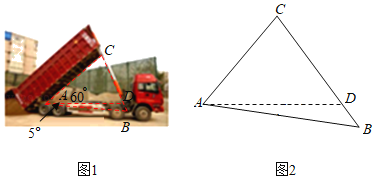
（参考数据：sin65°≈0.91，cos65°≈0.42，tan65°≈2.14，sin70°≈0.94，cos70°≈0.34，tan70°≈2.75，
≈1.41）
【答案】所求BC的长度约为2.6米．
【解析】
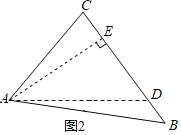
过点A作AE⊥BC于点E，先求出∠C，再运用锐角三角函数关系的知识求得CE和AE，然后再说明△AEB是等腰直角三角形得到AE＝BE，最后根据BC＝BE+CE解答即可．
解：如图，过点A作AE⊥BC于点E，
∵在Rt△ACE中，∠C＝180°﹣65°﹣45°＝70°，
∴cosC＝cos70°＝
，即CE＝AC×cos70°≈2×0.34＝0.68，
sinC＝sin70°＝
，AE＝AC×sin70°≈2×0.94＝1.88，
又∵在Rt△AEB中，∠ABC＝45°，
∴△AEB是等腰直角三角形
∴AE＝BE，
∴BC＝BE+CE＝0.68+1.88＝2.56≈2.6，
答：所求BC的长度约为2.6米．
练习册系列答案
相关题目
