ЬтФПФкШн
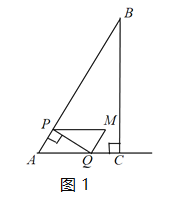
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯC=90ЁуЃЌAC=2cmЃЌAB=4cmЃЎЕуPДгЕуAГіЗЂЃЌбиABвд1cm/sЕФЫйЖШЯђжеЕуBдЫЖЏЃЎЕБЕуPгыЕуAЁЂBВЛжиКЯЪБЃЌЙ§ЕуPзїPQЁЭABНЛЩфЯпACгкЕуQЃЌвдAPЃЌAQЮЊСкБпЯђЩЯзїЦНааЫФБпаЮAPMQЃЎЩшЕуPЕФдЫЖЏЪБМфЮЊxЃЈsЃЉЃЌНтД№ЯТСаЮЪЬтЃЎ
ЃЈ1ЃЉЁЯA=ЁЁ ЁЁЁуЃЛ
ЃЈ2ЃЉЕБЕуMдкBCЩЯЪБЃЌxЕФжЕЮЊЁЁ ЁЁЃЛ
ЃЈ3ЃЉЩшЦНааЫФБпаЮAPMQгыЁїABCЕФжиЕўВПЗжЭМаЮЕФУцЛ§ЮЊyЃЈcm2ЃЉЃЌЧѓyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ4ЃЉећИідЫЖЏЙ§ГЬжаЃЌжБНгаДГіЁїABMЮЊжБНЧШ§НЧаЮЪБxЕФжЕЃЎ
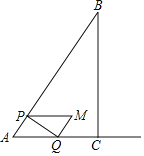
ЁОД№АИЁПЃЈ1ЃЉ60ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ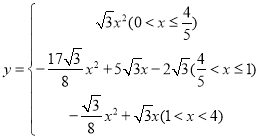 ЃЛЃЈ4ЃЉ
ЃЛЃЈ4ЃЉ![]() Лђ2
Лђ2
ЁОНтЮіЁП
ЃЈ1ЃЉЧѓГіЁЯAЕФгрЯвжЕМДПЩНтОіЮЪЬтЃЎ
ЃЈ2ЃЉРћгУЦНааЯпЗжЯпЖЮГЩБШР§ЖЈРэЃЌЙЙНЈЗНГЬЧѓНтМДПЩЃЎ
ЃЈ3ЃЉЗжШ§жжЧщаЮЃКШчЭМ1жаЃЌЕБ0ЃМxЁм![]() ЪБЃЌжиЕўВПЗжЪЧЦНааЫФБпаЮAPMQЃЎШчЭМ3жаЃЌЕБ
ЪБЃЌжиЕўВПЗжЪЧЦНааЫФБпаЮAPMQЃЎШчЭМ3жаЃЌЕБ![]() ЃМxЁм1ЪБЃЌжиЕўВПЗжЪЧЮхБпаЮAPEFQЃЎШчЭМ4жаЃЌЕБ1ЃМxЃМ4ЪБЃЌжиЕўВПЗжЪЧЫФБпаЮAPECЃЎЗжБ№ЧѓНтМДПЩНтОіЮЪЬтЃЎ
ЃМxЁм1ЪБЃЌжиЕўВПЗжЪЧЮхБпаЮAPEFQЃЎШчЭМ4жаЃЌЕБ1ЃМxЃМ4ЪБЃЌжиЕўВПЗжЪЧЫФБпаЮAPECЃЎЗжБ№ЧѓНтМДПЩНтОіЮЪЬтЃЎ
ЃЈ4ЃЉЗжСНжжЧщаЮЃКЂйЕБЁЯAMB=90ЁуЃЌРћгУЯрЫЦШ§НЧаЮЕФаджЪЙЙНЈЗНГЬЧѓНтЃЎЂкЕБЁЯABM=90ЁуЪБЃЌРћгУШ§НЧаЮЕФжаЮЛЯпЖЈРэЧѓНтМДПЩЃЎ
ЃЈ1ЃЉШчЭМжаЃЌ
дкRtЁїABCжаЃЌЁпЁЯACB=90ЁуЃЌAC=2cmЃЌAB=4cmЃЌ
ЁрcosA=![]() ЃЌ
ЃЌ
ЁрЁЯA=60ЁуЃЌ
ЙЪД№АИЮЊЃК60ЃЎ
ЃЈ2ЃЉШчЭМ2жаЃЌЕБЕуMТфдкBCЩЯЪБЃЌ
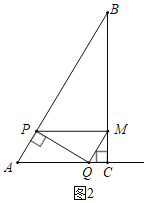
гЩЬтвтжЊЃЌPA=xcmЃЌ
ЁпЫФБпаЮAPMQЪЧЦНааЫФБпаЮЃЌ
ЁрPM=AQ=2AP=2xЃЌ
ЁпPMЁЮACЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёрx=![]() ЃЎ
ЃЎ
ЙЪД№АИЮЊЃК![]() ЃЎ
ЃЎ
ЃЈ3ЃЉШчЭМ1жаЃЌЕБ0ЃМxЁм![]() ЪБЃЌжиЕўВПЗжЪЧЦНааЫФБпаЮAPMQЃЌ
ЪБЃЌжиЕўВПЗжЪЧЦНааЫФБпаЮAPMQЃЌ
дкRtЁїAPQжаЃЌЁпЁЯAQP=30ЁуЃЌAP=xЃЌ
ЁрAQ=2xЃЌPQ=![]() xЃЌ
xЃЌ
Ёрy=SAPMQ=APЁСPQ=![]() x2ЃЎ
x2ЃЎ
ШчЭМ3жаЃЌЕБ![]() ЃМxЁм1ЪБЃЌжиЕўВПЗжЪЧЮхБпаЮAPEFQЃЌAP=xЃЌ
ЃМxЁм1ЪБЃЌжиЕўВПЗжЪЧЮхБпаЮAPEFQЃЌAP=xЃЌ
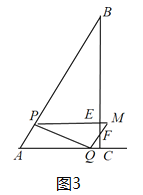
ЁрAQ=PM=2xЃЌPB=4ЉxЃЌ
ЁрPE=![]() ЃЈ4ЉxЃЉЃЎ
ЃЈ4ЉxЃЉЃЎ
ЁрEM=PMЉPE=2xЉ![]() ЃЈ4ЉxЃЉ=
ЃЈ4ЉxЃЉ=![]() xЉ2ЃЌ
xЉ2ЃЌ
ЁрEF=![]() ЃЈ
ЃЈ![]() xЉ2ЃЉЃЎ
xЉ2ЃЉЃЎ
Ёрy=SAPMQЉSЁїEFM=![]() x2Љ
x2Љ![]() ЁС
ЁС![]() ЃЈ
ЃЈ![]() xЉ2ЃЉ2=Љ
xЉ2ЃЉ2=Љ![]() x2+5
x2+5![]() xЉ2
xЉ2![]() ЃЎ
ЃЎ
ШчЭМ4жаЃЌЕБ1ЃМxЃМ4ЪБЃЌжиЕўВПЗжЪЧЫФБпаЮAPEBЃЌAP=xЃЌ

ЁрAQ=2xЃЌBP=4ЉxЃЌ
ЁрPE=![]() ЃЈ4ЉxЃЉЃЎ
ЃЈ4ЉxЃЉЃЎ
ЁрBE=![]() ЃЈ4ЉxЃЉЃЌ
ЃЈ4ЉxЃЉЃЌ
ЁрCE=2![]() Љ
Љ![]() ЃЈ4ЉxЃЉ=
ЃЈ4ЉxЃЉ=![]() xЃЎ
xЃЎ
Ёрy=SЫФБпаЮACEP=![]() ЃЈPE+ACЃЉCE=
ЃЈPE+ACЃЉCE=![]() [
[![]() ЃЈ4ЉxЃЉ+2]ЁС
ЃЈ4ЉxЃЉ+2]ЁС![]() x=Љ
x=Љ![]() x2+
x2+![]() xЃЎ
xЃЎ
злЩЯЫљЪіЃЌy=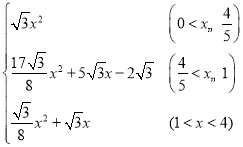 ЃЎ
ЃЎ
ЃЈ4ЃЉШчЭМ5жаЃЌЕБЁЯAMB=90ЁуЪБЃЌЩшPQНЛAMгкFЃЌ
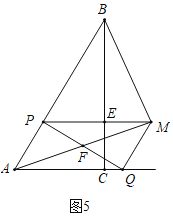
ЁпЁЯPAF=ЁЯBAMЃЌЁЯAPF=ЁЯAMB=90ЁуЃЌ
ЁрЁїAPFЁзЁїAMBЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпPA=xЃЌPQ=![]() xЃЌPF=FQ=
xЃЌPF=FQ=![]() xЃЌ
xЃЌ
ЁрAF=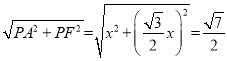 xЃЌ
xЃЌ
ЁпЫФБпаЮAPMQЪЧЦНааЫФБпаЮЃЌ
ЁрAM=2AF=![]() xЃЌ
xЃЌ
Ёр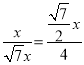 ЃЌ
ЃЌ
Ёрx=![]() ЃЌ
ЃЌ![]() ЃЈЩсШЅЃЉЃЎ
ЃЈЩсШЅЃЉЃЎ
ШчЭМ6жаЃЌЕБЁЯABM=90ЁуЪБЃЌЩшAMНЛPQгкFЃЎ
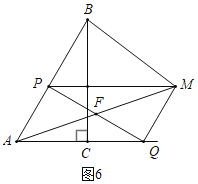
ЁпЁЯAPF=ЁЯABM=90ЁуЃЌ
ЁрPFЁЮBMЃЌ
ЁпAF=FMЃЌ
ЁрAP=PB=2ЃЌ
Ёрx=2ЃЌ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФxЕФжЕЮЊ![]() Лђ2ЃЎ
Лђ2ЃЎ