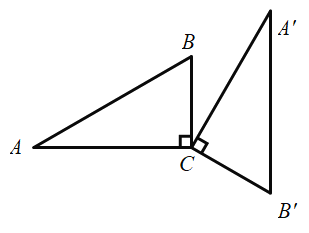
题目内容
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() ,
,![]() 为
为![]() 的切线,直线
的切线,直线![]() 交
交![]() 延长线于
延长线于![]() ,
,![]() .
.
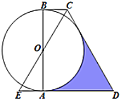
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求阴影部分的周长.
,求阴影部分的周长.
【答案】(1)证明见解析;(2)阴影部分的周长是![]()
【解析】
(1)过点O作OH⊥CD,垂足为H,连接OD,先证明![]() BOC≌
BOC≌![]() AOE(ASA),可得OC=OE,进而可证得OH=OB,再结合OH⊥CD即可得证;
AOE(ASA),可得OC=OE,进而可证得OH=OB,再结合OH⊥CD即可得证;
(2)先根据![]() 求得
求得![]() ,再证得∠AOH=∠DOA+∠DOH=120°,进而利用解直角三角形求得
,再证得∠AOH=∠DOA+∠DOH=120°,进而利用解直角三角形求得![]() ,利用弧长公式计算弧长即可求得答案.
,利用弧长公式计算弧长即可求得答案.
(1)证明:如图,过点O作OH⊥CD,垂足为H,连接OD,
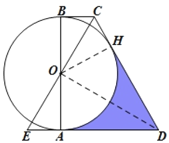
∵BC,AD为⊙O的切线,
∴∠CBO=∠OAE=90°,
又OB=OA,∠BOC=∠EOA,
∴![]() BOC≌
BOC≌![]() AOE(ASA),
AOE(ASA),
∴OC=OE,
又DC=DE,
∴DO平分∠ADE,OD⊥CE,
∴OH=OA,
∴OH=OB,
又∵OH⊥CD,
∴CD是⊙O的切线;
(2)解:∵在Rt![]() AEO中,∠E=60°,
AEO中,∠E=60°,
∴![]()
∵AE=1,
∴![]() ,
,
∵OD⊥CE,
∴∠DOA=90°-∠EOA=∠E=60°,
∠DOH=90°-∠COH=90°-∠COB=90°-∠AOE=∠E=60°,
![]() ,
,
∴弧AH的长是![]() ,
,
∴阴影部分的周长是![]() .
.

练习册系列答案
相关题目