Question

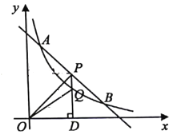
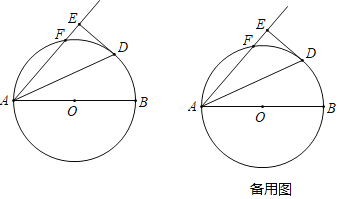
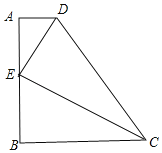
【题目】如图，已知梯形ABCD中，AD∥BC，AB⊥BC，AD＜BC，AB＝BC＝1，E是边AB上一点，联结CE．

（1）如果CE＝CD，求证：AD＝AE；

（2）联结DE，如果存在点E，使得△ADE、△BCE和△CDE两两相似，求AD的长；

（3）设点E关于直线CD的对称点为M，点D关于直线CE的对称点为N，如果AD＝，且M在直线AD上时，求的值．

Answer 1

【答案】（1）见解析；（2）；（3）．

【解析】

（1）过C点作CF⊥AD，交AD的延长线于F，可证ABCF是正方形，即AB=BC=CF=FA;再由“HL”证得Rt△CBE≌Rt△ CFD，可得BE=FD，最后用线段的和差即可；

（2）分∠EDC＝90°和∠DEC＝90°两种情况讨论，运用相似三角形的性质和直角三角形的性质即可求解；

（3）连接EM交CD于Q，连接DN交CE于P，连接ED，CM，作CF⊥AD于F，由轴对称的性质可得∠CPD=∠CQE=90°，DC垂直平分EM，可证Rt△CBE≌Rt△CFM，可得BE=FM，由勾股定理可求BE、CE的长，通过证明△CDP∽△CEQ，最后运用相似三角形的性质即可解答．

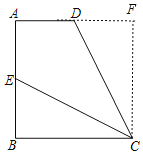
（1）证明：如图，过C点作CF⊥AD，交AD的延长线于F，

∵AD∥BC，AB⊥BC，AB＝BC，

∴四边形ABCF是正方形，

∴AB＝BC＝CF＝FA，

又∵CE＝CD，

∴Rt△CBE≌Rt△CFD（HL），

∴BE＝FD，

∴AD＝AE；

（2）①若∠EDC＝90°时，

若△ADE、△BCE和△CDE两两相似，

那么∠A＝∠B＝∠EDC＝90°，∠ADE＝∠BCE＝∠DCE＝30°，

在△CBE中，∵BC＝1，

∴，，

∵AB＝1，

∴，

∴，

此时≠，

∴△CDE与△ADE、△BCE不相似；

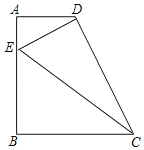
②如图，若∠DEC＝90°时，

∵∠ADE+∠A＝∠BEC+∠DEC，∠DEC＝∠A＝90°，

∴∠ADE＝∠BEC，且∠A＝∠B＝90°，

∴△ADE∽△BEC，

∴∠AED＝∠BCE，

若△CDE与△ADE相似，

∵AB与CD不平行，

∴∠AED与∠EDC不相等，

∴∠AED＝∠BCE＝∠DCE，

∴若△CDE与△ADE、△BCE相似，

∴，

∴AE＝BE，

∵AB＝1，

∴AE＝BE＝，

∴AD＝；

（3）连接EM交CD于Q，连接DN交CE于P，连接ED，CM，作CF⊥AD于F，

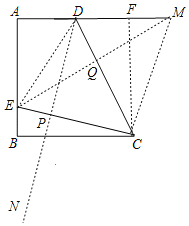
∵E关于直线CD的对称点为M，点D关于直线CE的对称点为N，

∴∠CPD＝∠CQE＝90°，DC垂直平分EM，

∠PCD＝∠QCE，

∴△CDP∽△CEQ，

∴，

∵AD∥BC，AB⊥BC，，AB＝BC＝1，

∴，

∵CD垂直平分EM，

∴DE＝DM，CE＝CM，

在Rt△CBE和Rt△CFM中，CB＝CF，EC＝CM，

∴Rt△CBE≌Rt△CFM（HL）

∴BE＝FM，

设BE＝x，则FM＝x，

∵ED＝DM，且AE2+AD2＝DE2，

∴，

∴，

∴，

∴，

∵DN＝2DP，EM＝2EQ，

∴．