题目内容
【题目】如图，在等边三角形
中，在
边上取两点
、
，使
．若
，
，
， 则以
，
，
为边长的三角形的形状为（ ）
A.锐角三角形B.直角三角形C.钝角三角形D.随，
，的值而定
【答案】C
【解析】
将△ABM绕点B顺时针旋转60
得到△CBH．连接HN．想办法证明∠HCN＝120，HN＝MN＝x即可解决问题；
将△ABM绕点B顺时针旋转60得到△CBH．连接HN．
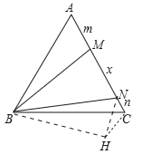
∵△ABC是等边三角形，
∴∠ABC＝∠ACB＝∠A＝60，
∵∠MON＝30，
∴∠ABM＋∠CBN＝30，
∴∠NBH＝∠CBH＋∠CBN＝30，
∴∠NBM＝∠NBH，
∵BM＝BH，BN＝BN，
∴△NBM≌△NBH，
∴MN＝NH＝x，
∵∠BCH＝∠A＝60，CH＝AM＝n，
∴∠NCH＝120，
∴x，m，n为边长的三角形△NCH是钝角三角形，
故选：C．
练习册系列答案
相关题目
【题目】某校组织了全校1500名学生参加传统文化知识网络竞赛．赛后随机抽取了其中200名学生的成绩作为样本进行整理，并制作了如下不完整的频数分布表和频数分布直方图．
成绩（分） | 频数（人） | 频率 |
50≤x＜60 | 10 | 0.05 |
60≤x＜70 | 20 | n |
70≤x＜80 | m | 0.15 |
80≤x＜90 | 80 | 0.40 |
90≤x＜100 | 60 | 0.30 |
请根据图表提供的信息，解答下列各题：
（1）表中m＝ ，n＝ ，请补全频数分布直方图；
（2）若用扇形统计图来描述成绩分布情况，则分数段80≤x＜90对应扇形的圆心角的度数是 ；
（3）若成绩在80分以上（包括80分）为合格，则参加这次竞赛的1500名学生中成绩合格的大约有多少名？
