题目内容
【题目】某校组织了全校1500名学生参加传统文化知识网络竞赛.赛后随机抽取了其中200名学生的成绩作为样本进行整理,并制作了如下不完整的频数分布表和频数分布直方图.
成绩(分) | 频数(人) | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 20 | n |
70≤x<80 | m | 0.15 |
80≤x<90 | 80 | 0.40 |
90≤x<100 | 60 | 0.30 |
请根据图表提供的信息,解答下列各题:
(1)表中m= ,n= ,请补全频数分布直方图;
(2)若用扇形统计图来描述成绩分布情况,则分数段80≤x<90对应扇形的圆心角的度数是 ;
(3)若成绩在80分以上(包括80分)为合格,则参加这次竞赛的1500名学生中成绩合格的大约有多少名?

【答案】(1)m=30、n=0.1,补全图形如下见解析;(2)144°;(3)参加这次竞赛的1500名学生中成绩合格的大约有1050人.
【解析】
(1)由0.15×200求得m,由20÷200求得n;再根据求得的数据补全直方图;
(2)用360°×0.40即可得到答案;
(3)用成绩80分以上的频率(0.40+0.30)乘以总人数即可得到答案.
(1)m=0.15×200=30、n=20÷200=0.1,补全图形如下:
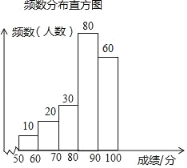
故答案为:30、0.1;
(2)分数段80≤x<90对应扇形的圆心角的度数是360°×0.40=144°,
故答案为:144°;
(3)参加这次竞赛的1500名学生中成绩合格的大约有1500×(0.40+0.30)=1050人.

【题目】二次函数y=ax2+bx+c (a、b、c为常数且a≠0)中的x与y的部分对应值如下表,
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 12 | 5 | 0 | -3 | -4 | -3 | 0 | 5 | 12 | … |
下列四个结论:
①二次函数y=ax2+bx+c 有最小值,最小值为-3;
②抛物线与y轴交点为(0,-3);
③二次函数y=ax2+bx+c 的图像对称轴是x=1;
④本题条件下,一元二次方程ax2+bx+c的解是x1=-1,x2=3.
其中正确结论的个数是( )
A.4
B.3
C.2
D.1
【题目】为了加强学生课外阅读,开阔视野,某校开展了“书香校园,从我做起”的主题活动.学校随机抽取了部分学生,对他们一周的课外阅读时间进行调查,绘制出频数分布表和频数分布直方图的一部分如下:
课外阅读时间(单位:小时) | 频数(人数) | 频率 |
0﹤t≤2 | 2 | 0.04 |
2﹤t≤4 | 3 | 0.06 |
4﹤t≤6 | 15 | 0.30 |
6﹤t≤8 | a | 0.50 |
t﹥8 | 5 | b |

请根据图表信息回答下列问题:
(1)频数分布表中的a=b=;
(2)将频数分布直方图补充完整;
(3)学校将每周课外阅读时间在8小时以上的学生评为“阅读之星”,请你估计该校2000名学生中评为“阅读之星”的有多少人?




