ĖâÄŋÄÚČÝ
ĄūĖâÄŋĄŋČįÍžĢŽ―ŦÆ―ÐÐËÄąßÐÎÖ―ÆŽ![]() ŅØķÔ―ĮÏß
ŅØķÔ―ĮÏß![]() ·ÕÛĢŽĘđĩã
·ÕÛĢŽĘđĩã![]() ÂäÔÚÆ―ÐÐËÄąßÐÎ
ÂäÔÚÆ―ÐÐËÄąßÐÎ![]() ËųÔÚÆ―ÃæÄÚĢŽ
ËųÔÚÆ―ÃæÄÚĢŽ![]() šÍ
šÍ![]() Ïā―ŧÓÚĩã
Ïā―ŧÓÚĩã![]() ĢŽÁŽ―Ó
ĢŽÁŽ―Ó![]()
![]() ÅÐķÏ
ÅÐķÏ![]() šÍ
šÍ![]() ĩÄÎŧÖÃđØÏĩĢŽēĒÖĪÃũĢŪ
ĩÄÎŧÖÃđØÏĩĢŽēĒÖĪÃũĢŪ
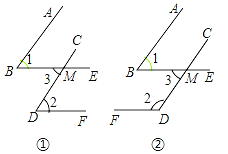
![]() ÔÚÍž1ÖÐĢŽČô
ÔÚÍž1ÖÐĢŽČô![]() ĢŽĘĮ·ņīæÔÚ
ĢŽĘĮ·ņīæÔÚ![]() ĮĄšÃΊֹ―ĮČý―ĮÐÎĩÄĮéÐÎ?ČôīæÔÚĢŽĮóģö
ĮĄšÃΊֹ―ĮČý―ĮÐÎĩÄĮéÐÎ?ČôīæÔÚĢŽĮóģö![]() ĩÄģĪķČĢšČôēŧīæÔÚĢŽĮëËĩÃũĀíÓÉĢŪ
ĩÄģĪķČĢšČôēŧīæÔÚĢŽĮëËĩÃũĀíÓÉĢŪ
![]() Čô―ŦÍžÖÐÆ―ÐÐËÄąßÐÎÖ―ÆŽ
Čô―ŦÍžÖÐÆ―ÐÐËÄąßÐÎÖ―ÆŽ![]() ŧŧģÉūØÐÎÖ―ÆŽ
ŧŧģÉūØÐÎÖ―ÆŽ![]() ĢŽŅØķÔ―ĮÏßÕÛĩþ·ĒÏÖËųĩÃÍžÐÎĘĮÖáķÔģÆÍžÐÎĢŧ―ŦËųĩÃÍžÐÎŅØÆäķÔģÆÖáÔŲīÎÕÛĩþšóĢŽĩÃĩ―ĩÄČÔĘĮÖáķÔģÆÍžÐÎĢŪÔōūØÐÎÖ―ÆŽ
ĢŽŅØķÔ―ĮÏßÕÛĩþ·ĒÏÖËųĩÃÍžÐÎĘĮÖáķÔģÆÍžÐÎĢŧ―ŦËųĩÃÍžÐÎŅØÆäķÔģÆÖáÔŲīÎÕÛĩþšóĢŽĩÃĩ―ĩÄČÔĘĮÖáķÔģÆÍžÐÎĢŪÔōūØÐÎÖ―ÆŽ![]() ĩÄģĪŋíÖŪąČĘĮķāÉŲ?ĮëÖą―ÓÐīģö―áđûĢŪ
ĩÄģĪŋíÖŪąČĘĮķāÉŲ?ĮëÖą―ÓÐīģö―áđûĢŪ

Ąūīð°ļĄŋĢĻ1ĢĐÆ―ÐÐĢŽĀíÓÉžû―âÎöĢĻ2ĢĐīæÔÚĩąBCĩÄģĪΊ2ŧō3ŧō6ŧō4ĘąĢŽĄũABĄäDĘĮÖą―ĮČý―ĮÐÎĢĻ3ĢĐūØÐÎÖ―ÆŽABCDĩÄģĪŋíÖŪąČĘĮ1Ģš1ŧō![]() Ģš1
Ģš1
Ąū―âÎöĄŋ
ĢĻ1ĢĐÓÉÕÛĩþÖŠBCĢ―BĄäCĢŽĄÏACBĢ―ĄÏACBĄäĢŽ―ášÏĄÏACBĢ―ĄÏCADÖŠĄÏACBĄäĢ―ĄÏCADĢŽĩÃAEĢ―CEĢŽÔŲÓÉBCĢ―BĄäCĢ―ADÖŠDEĢ―BĄäEĢŽīÓķøĩÃĄÏEDBĄäĢ―ĄÏEBĄäDĢŽļųūÝĄÏAECĢ―ĄÏDEBĄäĩÃĄÏACBĄäĢ―ĄÏCADĢ―ĄÏEDBĄäĢ―ĄÏEBĄäDĢŽīÓķøĩÃÖĪĢŪ
ĢĻ2ĢĐÏČÖĪĩÃËÄąßÐÎACBĄäDĘĮĩČŅüĖÝÐÎĢŽ·ÖËÄÖÖĮéÐηֹðĖÖÂÛĮó―âžīŋÉ―âūöÎĘĖâĢŧ
ĢĻ3ĢĐĒŲĩąABĢšADĢ―1Ģš1ĘąĢŽ·ûšÏĖâŌâĢŪĒÚĩąADĢšABĢ―![]() Ģš1ĘąĢŽŌē·ûšÏĖâŌâĢŽļųūÝČŦĩČČý―ĮÐÎĩÄÅÐķĻÓëÐÔÖĘž°šŽ30ĄãĩÄÖą―ĮČý―ĮÐÎĩÄÐÔÖĘžīŋÉĮó―âĢŪ
Ģš1ĘąĢŽŌē·ûšÏĖâŌâĢŽļųūÝČŦĩČČý―ĮÐÎĩÄÅÐķĻÓëÐÔÖĘž°šŽ30ĄãĩÄÖą―ĮČý―ĮÐÎĩÄÐÔÖĘžīŋÉĮó―âĢŪ
ĢĻ1ĢĐBĄäDĄÎACĢŽ
ĄßËÄąßÐÎABCDĘĮÆ―ÐÐËÄąßÐÎĢŽ
ĄāADĢ―BCĢŽADĄÎBCĢŽ
ĄāĄÏACBĢ―ĄÏCADĢŽ
ÓÉÕÛĩþÖŠBCĢ―BĄäCĢŽĄÏACBĢ―ĄÏACBĄäĢŽ
ĄāĄÏACBĄäĢ―ĄÏCADĢŽ
ĄāAEĢ―CEĢŽ
ÓÖĄßBCĢ―BĄäCĢ―ADĢŽ
ĄāDEĢ―BĄäEĢŽ
ĄāĄÏEDBĄäĢ―ĄÏEBĄäDĢŽ
ĄßĄÏAECĢ―ĄÏDEBĄäĢŽ
ĄāĄÏACBĄäĢ―ĄÏCADĢ―ĄÏEDBĄäĢ―ĄÏEBĄäDĢŽ
ĄāBĄäDĄÎACĢŧ
ĢĻ2ĢĐĄßADĢ―BCĢŽBCĢ―BĄäCĢŽ
ĄāADĢ―BĄäCĢŽ
ĄßACĄÎBĄäDĢŽ
ĄāËÄąßÐÎACBĄäDĘĮĩČŅüĖÝÐÎĢŽ
ĄßĄÏBĢ―30ĄãĢŽ
ĄāĄÏABĄäCĢ―ĄÏCDAĢ―30ĄãĢŽ
ĩąĄÏBĄäADĢ―90ĄãĢŽABĢūBCĘąĢŽČįÍž1ÖÐĢŽ

ÉčĄÏADBĄäĢ―ĄÏCBĄäDĢ―yĢŽ
ĄāĄÏABĄäDĢ―y30ĄãĢŽ
―âĩÃyĢ―60ĄãĢŽ
ĄāĄÏABĄäDĢ―y30ĄãĢ―30ĄãĢŽ
ĄßABĄäĢ―ABĢ―2![]() ĢŽÉčAD=xĢŽÔōBĄŊD=2x
ĢŽÉčAD=xĢŽÔōBĄŊD=2x
ĄāBĄŊD2=AD2+ABĄŊ2ĢŽžīĢĻ2xĢĐ2=x2+(2![]() )2ĢŽ―âĩÃx=2
)2ĢŽ―âĩÃx=2
ĄāADĢ―2ĢŽ
ĄāBCĢ―2Ģŧ
ĩąĄÏADBĄäĢ―90ĄãĢŽABĢūBCĘąĢŽČįÍž2ĢŽ
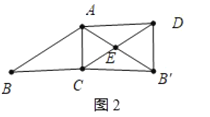
ĄßADĢ―BCĢŽBCĢ―BĄäCĢŽ
ĄāADĢ―BĄäCĢŽ
ĄßACĄÎBĄäDĢŽ
ĄāËÄąßÐÎACBĄäDĘĮĩČŅüĖÝÐÎĢŽ
ĄßĄÏADBĄäĢ―90ĄãĢŽ
ĄāËÄąßÐÎACBĄäDĘĮūØÐÎĢŽ
ĄāĄÏACBĄäĢ―90ĄãĢŽ
ĄāĄÏACBĢ―90ĄãĢŽ
ĄßĄÏBĢ―30ĄãĢŽABĢ―2![]() ĢŽ
ĢŽ
ĄāAC=![]() AB=
AB=![]()
ĄāBCĢ―![]() Ģ―3Ģŧ
Ģ―3Ģŧ
ĩąĄÏBĄäADĢ―90ĄãĢŽABĢžBCĘąĢŽČįÍž3ĢŽ

ĄßADĢ―BCĢŽBCĢ―BĄäCĢŽ
ĄāADĢ―BĄäCĢŽ
ĄßACĄÎBĄäDĢŽĄÏBĄäADĢ―90ĄãĢŽ
ĄßĄÏBĢ―30ĄãĢŽABĄäĢ―2![]() ĢŽ
ĢŽ
ĄāĄÏABĄäCĢ―30ĄãĢŽ
ĄāAE=![]() BĄŊEĢŽBĄŊE=2AEĢŽ
BĄŊEĢŽBĄŊE=2AEĢŽ
ĄāBĄŊE2=AE2+ABĄŊ2ĢŽžīĢĻ2AEĢĐ2=AE2+(2![]() )2ĢŽ
)2ĢŽ
ĄāAEĢ―2ĢŽBĄŊEĢ―2AEĢ―4ĢŽ
ĄßĄÏACBĢ―ĄÏACBĄŊ=ĄÏCAD =30Ąã
ĄāAEĢ―ECĢ―2ĢŽ
ĄāCBĄäĢ―6ĢŽ
ĩąĄÏABĄäDĢ―90ĄãĘąĢŽČįÍž4ĢŽ
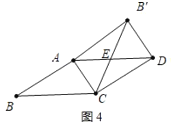
ĄßADĢ―BCĢŽBCĢ―BĄäCĢŽ
ĄāADĢ―BĄäCĢŽ
ĄßACĄÎBĄäDĢŽ
ĄāËÄąßÐÎACDBĄäĘĮÆ―ÐÐËÄąßÐÎĢŽ
ĄßĄÏABĄäDĢ―90ĄãĢŽ
ĄāËÄąßÐÎACDBĄäĘĮūØÐÎĢŽ
ĄāĄÏBACĢ―90ĄãĢŽ
ĄßĄÏBĢ―30ĄãĢŽABĢ―2![]() ĢŽ
ĢŽ
ĄāBC=2ACĢŽAC=![]() BC
BC
ĄāBC2=AC2+AB2ĢŽžīĢĻBCĢĐ2=ĢĻ![]() BCĢĐ2+(2
BCĢĐ2+(2![]() )2ĢŽ
)2ĢŽ
ĄāBCĢ―4Ģŧ
ĄāŌŅÖŠĩąBCĩÄģĪΊ2ŧō3ŧō6ŧō4ĘąĢŽĄũABĄäDĘĮÖą―ĮČý―ĮÐÎĢŪ
ĢĻ3ĢĐČįÍž5ÖÐĢŽ
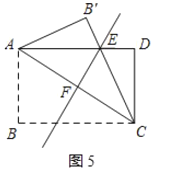
ĒŲĩąABĢšADĢ―1Ģš1ĘąĢŽËÄąßÐÎABCDĘĮÕý·―ÐÎĢŽ
ĄāĄÏBACĢ―ĄÏCADĢ―ĄÏEABĄäĢ―45ĄãĢŽ
ĄßAEĢ―AEĢŽĄÏBĄäĢ―ĄÏAFEĢ―90ĄãĢŽ
ĄāĄũAEBĄäĄÕĄũAEFĢĻAASĢĐĢŽ
ĄāABĄäĢ―AFĢŽ
īËĘąËÄąßÐÎAFEBĄäĘĮÖáķÔģÆÍžÐÎĢŽ·ûšÏĖâŌâĢŪ
ĒÚĩąADĢšABĢ―![]() Ģš1ĘąĢŽŌē·ûšÏĖâŌâĢŽ
Ģš1ĘąĢŽŌē·ûšÏĖâŌâĢŽ
ÔōAD=![]() AB
AB
ĄāAC=![]()
ĄāĄÏDAC=30ĄãĢŽ
ĄāACĢ―2CDĢŽ
ĄāAFĢ―FCĢ―CDĢ―ABĢ―ABĄäĢŽ
ĄāīËĘąËÄąßÐÎAFEBĄäĘĮÖáķÔģÆÍžÐÎĢŽ·ûšÏĖâŌâĢŪ
ŨÛÉÏĢŽūØÐÎÖ―ÆŽABCDĩÄģĪŋíÖŪąČĘĮ1Ģš1ŧō![]() Ģš1ĢŪ
Ģš1ĢŪ

 ŋÎĖÃČŦ―âŨÖīĘūäķÎÆŠÕÂÏĩÁÐīð°ļ
ŋÎĖÃČŦ―âŨÖīĘūäķÎÆŠÕÂÏĩÁÐīð°ļ ē―ē―ļßŋÚËãĖâŋĻÏĩÁÐīð°ļ
ē―ē―ļßŋÚËãĖâŋĻÏĩÁÐīð°ļ