题目内容
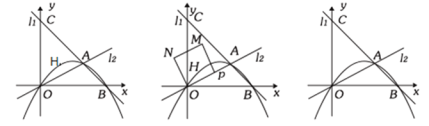
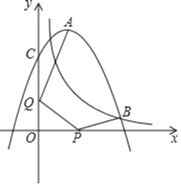
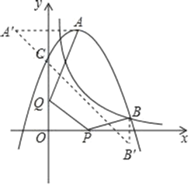
【题目】如图,抛物线y=ax2+4x+c(a≠0)与反比例函数y=![]() 的图象相交于点B,且点B的横坐标为5,抛物线与y轴交于点C(0,6),A是抛物线的顶点,P和Q分别是x轴和y轴上的两个动点,则AQ+QP+PB的最小值为_____.
的图象相交于点B,且点B的横坐标为5,抛物线与y轴交于点C(0,6),A是抛物线的顶点,P和Q分别是x轴和y轴上的两个动点,则AQ+QP+PB的最小值为_____.
【答案】![]()
【解析】
根据题意求得B的坐标,然后根据待定系数法求得抛物线的解析式,从而求得顶点A的坐标,求得A关于y轴的对称点A′(-2,10),B点关于x轴的对称点B′为(5,-1),根据两点之间线段最短,即可判断AQ+QP+PB=A′B′是AQ+QP+PB的最小值,利用勾股定理求得即可.
∵点B在反比例函数y=![]() 的图象,且点B的横坐标为5,
的图象,且点B的横坐标为5,
∴点B的纵坐标为:y=![]() =1,
=1,
∴B(5,1),
∵抛物线y=ax2+4x+c(a≠0)与反比例函数y=![]() 的图象相交于点B,与y轴交于点C(0,6),
的图象相交于点B,与y轴交于点C(0,6),
∴![]() ,解得
,解得![]() ,
,
∴抛物线为y=﹣x2+4x+6,
∵y=﹣x2+4x+6=﹣(x﹣2)2+10,
∴A(2,10),
∴A关于y轴的对称点A′(﹣2,10),
∵B(5,1),
∴B点关于x轴的对称点B′为(5,﹣1),
连接A′B′交x轴于P,交y轴于Q,此时AQ+QP+PB的值最小,即AQ+QP+PB=A′B′,
A′B′=![]() =
=![]() ,
,
故AQ+QP+PB的最小值为![]() .
.

【题目】某农科所在相同条件下做某作物种子发芽率的实验,结果如下表所示:
种子个数 | 200 | 300 | 500 | 700 | 800 | 900 | 1000 |
发芽种子个数 | 187 | 282 | 435 | 624 | 718 | 814 | 901 |
发芽种子率 | 0.935 | 0.940 | 0.870 | 0.891 | 0.898 | 0.904 | 0.901 |
下面有四个推断:
①种子个数是700时,发芽种子的个数是624,所以种子发芽的概率是0.891;
②随着参加实验的种子数量的增加,发芽种子的频率在0.9附近摆动,显示出一定的稳定性,可以估计种子发芽的概率约为0.9(精确到0.1);
③实验的种子个数最多的那次实验得到的发芽种子的频率一定是种子发芽的概率;
④若用频率估计种子发芽的概率约为0.9,则可以估计![]() 种子中大约有
种子中大约有![]() 的种子不能发芽.
的种子不能发芽.
其中合理的是______.
【题目】某超市销售一种商品,成本每千克30元,规定每千克售价不低于成本,且不高于70元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 40 | 50 | 60 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入成本);
(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少?