��Ŀ����
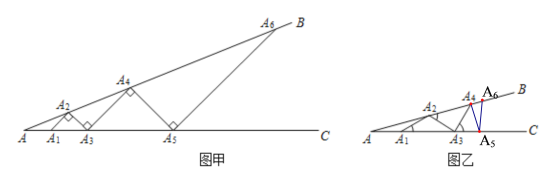
����Ŀ��ij��ѧ��ȤС�鿪չ��һ�λ���������£���![]() .�ְ�С�����ΰڷ���������֮�䣬��ʹС�����˷ֱ���������
.�ְ�С�����ΰڷ���������֮�䣬��ʹС�����˷ֱ���������![]() ��
��![]() �ϣ�
�ϣ�
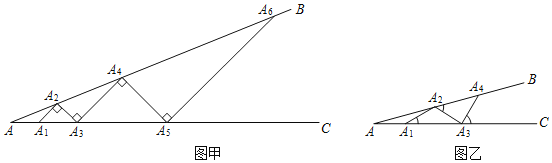
�һ����ͼ����ʾ���ӵ�![]() ��ʼ���������Ұڷ�С����ʹС����С���ڶ˵㴦���ഹֱ��
��ʼ���������Ұڷ�С����ʹС����С���ڶ˵㴦���ഹֱ��![]() Ϊ��1��С����
Ϊ��1��С����
��ѧ˼����
��1��С�������ް���ȥ�𣿴� ����ܡ����ܡ���
��2����![]() ����
����![]() �Ķ�����
�Ķ�����
�������ͼ����ʾ���ӵ�![]() ��ʼ���õȳ���С���������Ұڷţ�����
��ʼ���õȳ���С���������Ұڷţ�����![]() Ϊ��һ��С������
Ϊ��һ��С������![]() ��
��
��ѧ˼����
��3�����Ѿ��ڷ���3��С������![]() ��
��![]() ��
��![]() �����ú�
�����ú�![]() ��ʽ�ӱ�ʾ��
��ʽ�ӱ�ʾ��
��4����ֻ�ܰڷ�5��С������![]() ��ȡֵ��Χ�� ��
��ȡֵ��Χ�� ��
���𰸡���1���ܣ���2������22.5�㣻��3��2����3����4������4��15�������18�㣮
��������
��1����С����С���ڶ˵㴦���ഹֱ�����ɵõ��𰸣�
��2�����ݵ���ֱ�������ε����ʺ���������ǵ����ʣ����ɵõ��𰸣�
��3����![]() ���á�AA2A1=��A2AA1=�����Ӷ���
���á�AA2A1=��A2AA1=�����Ӷ���![]() ��AA2A1+��A2AA1=2����ͬ����
��AA2A1+��A2AA1=2����ͬ����![]() ��A2AA1+
��A2AA1+![]() =��+2��=3�ȣ�
=��+2��=3�ȣ�![]() ��A2AA1+
��A2AA1+![]() ��+3��=4�ȣ�
��+3��=4�ȣ�
��4����������ã�5����90����6����90�㣬�������ɵõ��𰸣�
��1����С����С���ڶ˵㴦���ഹֱ���ɣ�
��С�������ް���ȥ��
�ʴ��ǣ��ܣ�
��2����A1A2��A2A3��A1A2��A2A3��
���A2A1A3��45�㣬
���AA2A1+����45�㣬
��AA1��A1A2
���AA2A1����BAC=����
������22.5�㣻
��3����![]() ��
��
���AA2A1=��A2AA1=����
��![]() ��AA2A1+��A2AA1=2����
��AA2A1+��A2AA1=2����
��![]() ��
��
��![]()
![]() =2�ȣ�
=2�ȣ�
��![]() ��A2AA1+
��A2AA1+![]() =��+2��=3�ȣ�
=��+2��=3�ȣ�
��![]() ��
��
��![]()
![]() 3�ȣ�
3�ȣ�
��![]() ��A2AA1+
��A2AA1+![]() ��+3��=4�ȣ�
��+3��=4�ȣ�
�ʴ��ǣ�2����3����4����
��4���ɵڣ�3����ɵã�![]() 5�ȣ�
5�ȣ�![]() 6�ȣ�
6�ȣ�
��ֻ�ܰڷ�5��С����
��5����90����6����90�㣬
��15�������18�㣮
�ʴ��ǣ�15�������18�㣮