题目内容
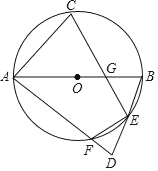
【题目】如图,AD,AC分别是⊙O的直径和弦.且∠CAD=30°.OB⊥AD交AC于点B.若OB=4,则BC长为( )
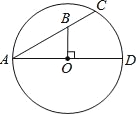
A. 2 B. 3 C. 3.6 D. 4
【答案】D
【解析】
首先连接CD,由圆周角定理可得∠C=90°,又由∠CAD=30°,OB⊥AD,OB=4,即可求得OA,AB的长,然后在Rt△ACD中,由三角函数的性质,即可求得答案.
解:连接CD,
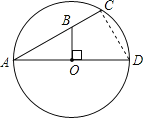
∵AD是⊙O的直径,
∴∠C=90°,
∵OB⊥AD,
∴∠AOB=∠C=90°,
在Rt△AOB中,∠CAD=30°,OB=4,
∴AB=2OB=8,OA=![]() =4
=4![]() ,
,
∴AD=2OA=8![]() ,
,
在Rt△ABC中,AC=ADcos30°=8![]() ×
×![]() =12,
=12,
∴BC=AC-AB=12-8=4.
故选:D.

练习册系列答案
相关题目