题目内容
【题目】已知:如图,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 的弦,
的弦,![]() 为
为![]() 上一点,过点
上一点,过点![]() 作
作![]() ,交弦
,交弦![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,且
,且![]() .
.
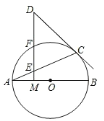
![]() 求证:
求证:![]() 是
是![]() 的切线;
的切线;
![]() 如果
如果![]() ,
,![]() ,
,![]() ,求
,求![]() 半径的长.
半径的长.
【答案】(1)详见解析;(2)![]() .
.
【解析】
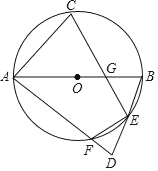
(1)连接OC,由OA=OC,DC=DE,利用等边对等角得到两对角相等,根据DM垂直于AC,得到一对角互余,等量代换得到∠OCD=90°,即可得到DC为圆O的切线;
(2)过D作DG垂直于AC,连接CB,利用三线合一得到G为CE中点,由CE长求出EG长,利用对顶角相等得到∠DEG=∠AEM,确定出cos∠DEG=cos∠AEM,在直角三角形DEG中,利用锐角三角函数定义求出DE的长,再利用勾股定理求出DG的长,由DM-DE求出EM的长,由一对直角相等,一对对顶角相等得到三角形AEM与三角形DEG相似,由相似得比例求出AM与AE的长,AE+EC求出AC的长,由AB为圆的直径,得到三角形ABC为直角三角形,利用锐角三角函数定义表示出cosA,即可求出AB的长,进而确定出圆的半径.
![]() 证明:如图,连结
证明:如图,连结![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是
是![]() 的切线;
的切线;
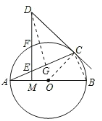
![]() 如图所示,过
如图所示,过![]() 作
作![]() ,连接
,连接![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 为圆
为圆![]() 的直径,
的直径,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
则圆![]() 的半径为
的半径为![]() .
.

练习册系列答案
相关题目