Question

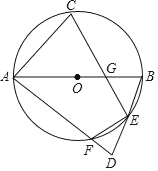
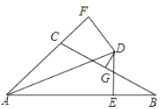
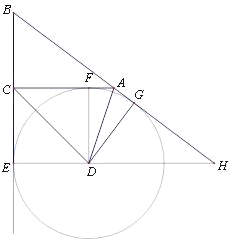
【题目】如图，在△ABC中，BC=a，AC=b，AB=c，⊙D与BC、AC、AB都相切，切点分别是E、F、G，BA、ED的延长线交于点H，a、b是关于x的方程x2﹣（c+4）x+4c+8=0的两个根．

(1)求证：△ABC是直角三角形；

(2)若25asin∠BAC=9c，求四边形CEDF的面积．

Answer 1

【答案】(1)证明见解析；(2)36．

【解析】

（1）根据根与系数的关系得到a+b=c+4，ab=4c+8，把第一等式两边平方后把第二个等式代入得到a2+b2=c2，根据勾股定理的逆定理即可得到结论；

（2）由25asin∠BAC=9c，即sin∠BAC=，再根据三角函数定义得sin∠BAC=，则3c=5a，设c=5x，则a=3x，b=4x，代入a+b=c+4求出x=2，则得到a=6，b=8，c=10；根据切线的性质得到DE=DF=DG，DE⊥BC，DG⊥AB，得到四边形DECF为正方形，设DE=DF=DG=R，利用S△ABC+S梯形DECA=S△BED+S△DAB，得到关于R的方程，解方程求出R，即可得到四边形CEDF的面积．

(1)∵a、b是关于x的方程x2﹣（c+4）x+4c+8=0的两个根，

∴a+b=c+4，ab=4c+8，

∴（a+b）2=（c+4）2，即a2+2ab+b2=c2+8c+16，

∴a2+b2=c2，

∴△ABC是直角三角形；

(2)连DB，如图

∵25asin∠BAC=9c，即sin∠BAC=，

在Rt△ABC中，sin∠BAC=，

∴=，

∴25a2=9c2，

∴3c=5a，

设c=5x，则a=3x，b=4x，

∴5x+4x=3x+4x+4，解得x=2，

∴a=6，b=8，c=10，

∵⊙D与BC、AC、AB都相切，切点分别是E、F、G，

∴DE=DF=DG，DE⊥BC，DG⊥AB，

∴四边形DECF为正方形，

设DE=DF=DG=R，

∵S△ABC+S梯形DECA=S△BED+S△DAB，

∴×6×8+×（R+8）×R=×（6+R）×R+×10×R，解得R=6，

∴四边形CEDF的面积=R2=36．