Question

【题目】如图，在Rt△ABC中，∠C=90°，BD是△ABC的一条角平分线．点O、E、F分别在BD、BC、AC上，且四边形OECF是正方形．

（1）求证：点O在∠BAC的平分线上；
（2）若AC=5，BC=12，求OE的长．

Answer 1

【答案】
（1）证明：过点O作OM⊥AB，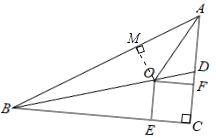

∵BD是∠ABC的一条角平分线，

∴OE=OM，

∵四边形OECF是正方形，

∴OE=OF，

∴OF=OM，

∴AO是∠BAC的角平分线，即点O在∠BAC的平分线上

（2）解：∵在Rt△ABC中，AC=5，BC=12，

∴AB= = =13，

设CE=CF=x，BE=BM=y，AM=AF=z，

∴ ，

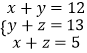解得： ，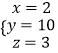

∴CE=2，

∴OE=2．

【解析】（1）过点O作OM⊥AB，根据角平分线的性质定理得出OE=OM，再根据正方形的性质得出OE=OF，从而得出OF=OM，，根据角平分线的判定定理得出结论；
（2）在Rt△ABC中，利用勾股定理得出AB的长，设CE=CF=x，BE=BM=y，AM=AF=z，根据切线长定理得出方程组，求解即可。
【考点精析】关于本题考查的切线长定理和角的平分线判定，需要了解从圆外一点引圆的两条切线，它们的切线长相等圆心和这一点的连线平分两条切线的夹角；可以证明三角形内存在一个点，它到三角形的三边的距离相等这个点就是三角形的三条角平分线的交点(交于一点)才能得出正确答案．