��Ŀ����
����Ŀ����ֱ������ϵxOy�У�ABCD�ĸ����������ֱ�ΪA��1��1����B��4��1����C��5��2����D��2��2����ֱ��l��y=kx+b��ֱ��y=��2xƽ�У�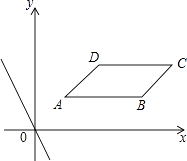
��1��k=��
��2����ֱ��l����D����ֱ��l�Ľ���ʽ��
��3����ֱ��lͬʱ���AB��CD���ཻ����b��ȡֵ��Χ��
��4����ֱ��l���߶�AC�ӵ�Aƽ������C����ֱ��l��x��Ľ���ΪP�����Ƿ����һ��P��ʹ��PABΪ���������Σ������ڣ�ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��-2
��2���⣺��ֱ��l�Ľ���ʽ��y=��2x+b��
�ѣ�2��2������ã���4+b=2����ã�b=6��
��ֱ��l�Ľ���ʽ��y=��2x+6
��3���⣺���Aֱ��l�Ľ���ʽ��y=��2x+b���ѣ�1��1������ã���2+c=1����ã�c=3��
��ֱ�ߵĽ���ʽ��y=��2x+3��
ͬ������Cֱ��l�Ľ���ʽ��y=��2x+12��
��3��b��12
��4���⣺ 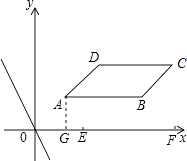
��ֱ��l����Aʱ������ʽ��y=��2x+3����y=0�����x= ![]() ������x��Ľ�����E��
������x��Ľ�����E�� ![]() ��0����
��0����
��ֱ��l����Cʱ������ʽ��y=��2x+12����y=0�����x=6������x��Ľ�����F��6��0����
��PA=PBʱ��P��AB���д����ϣ���P�������ǣ� ![]() ��0����
��0����
��AP=AB=3ʱ����PG= ![]() =2
=2 ![]() ����P�������ǣ�2
����P�������ǣ�2 ![]() +1��0����
+1��0����
ͬ������BP=BA=3ʱ��P�������ǣ�4��2 ![]() ��0����
��0����
��P�������ǣ��� ![]() ��0����2
��0����2 ![]() +1��0����4��2
+1��0����4��2 ![]() ��0����
��0����
����������1��������ֱ֪��l��y=kx+b��ֱ��y=��2xƽ�У�һ����ϵ����ͬ���ݴ˼�����á�
��2����ֱ��l�Ľ���ʽ��y=-2x+b����D������������ʽ�������b��ֵ�����ɵõ������Ľ���ʽ��
��3���ֱ���þ���A��C�Ľ���ʽ���������b��ȡֵ��Χ��
��4���ȷֱ������ֱ��l����Aʱ�͵�ֱ��l����Cʱ�ĺ�������ʽ���ٵ���PA=PB��AP=AB��BP=BA��������������ۼ�����⡣
�����㾫����������Ĺؼ���������ȷ��һ�κ����ı���ʽ�����֪ʶ������ȷ��һ��һ�κ�������Ҫȷ��һ�κ�������ʽy=kx+b��k������0���еij���k��b�������������һ�㷽���Ǵ���ϵ�������Լ��Ե��������ε����ʵ����⣬�˽���������ε���������ȣ���ƣ��ȱ߶ԵȽǣ���