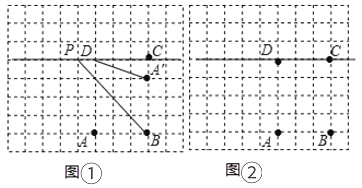
题目内容
【题目】在菱形![]() 中,
中,![]() 为直线
为直线![]() 上的点,
上的点,![]() 为直线
为直线![]() 上的点,分别连接
上的点,分别连接![]() ,
,![]() ,且
,且![]() .
.
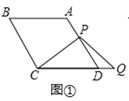
(1)若![]() ,点
,点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 的延长线上,如图①,易证:
的延长线上,如图①,易证:![]() (不需证明);
(不需证明);
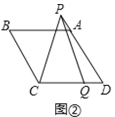
(2)如图②,若∠B=120°,点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
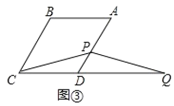
在线段![]() 的延长线上,如图③,猜想线段
的延长线上,如图③,猜想线段![]() ,
,![]() 和
和![]() 之间有怎样的数量关系?请直接写出对图②,图③的猜想,并选择其中一种情况给予证明.
之间有怎样的数量关系?请直接写出对图②,图③的猜想,并选择其中一种情况给予证明.
【答案】(1)见解析;(2)②结论:![]() ;③结论:
;③结论:![]() ,证明见解析
,证明见解析
【解析】
(1)连接AC,过P作PE∥CD交AC于E,由四边形ABCD是菱形,∠B=60°,得出△ACD是等边三角形,∠PDQ=120°,由PE∥CD,得出△APE是等边三角形,∠PEC=120°,由AAS证得△PCE≌△PQD,得出PE=DQ,AP=DQ,即可得出结论;
(2)①结论:![]() .如图②中,延长
.如图②中,延长![]() 到
到![]() ,使得
,使得![]() ,连接
,连接![]() .只要证明
.只要证明![]() 是等边三角形,
是等边三角形,![]() 即可解决问题;
即可解决问题;
②结论:![]() .如图③中,在
.如图③中,在![]() 上截取
上截取![]() ,连接
,连接![]() .只要证明
.只要证明![]() 是等边三角形,
是等边三角形,![]() 即可解决问题;
即可解决问题;
解:(1)证明:连接AC,过P作PE∥CD交AC于E,如图①所示:
∵四边形ABCD是菱形,
∴AD=CD=AB,∠ADC=∠B=60°,
∴△ACD是等边三角形,∠PDQ=120°,
∴AC=AD,∠DAC=∠ACD=60°,
∵PE∥CD,
∴∠AEP=∠ACD=60°,∠APE=∠ADC=60°,
∴△APE是等边三角形,∠PEC=120°,
∴AE=PE=AP,
∵PC=PQ,
∴∠PCQ=∠Q,
∵∠ACD=∠ECP+∠PCQ,∠ADC=∠DPQ+∠Q,
∴∠ECP=∠DPQ,
在△PCE和△PQD中,
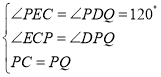 ,
,
∴△PCE≌△PQD(AAS),
∴PE=DQ,
∴AP=DQ,
∴DQ+PD=AP+PD=AD=AB;

(2)②结论:![]() .
.
理由:如图②中,延长![]() 到
到![]() ,使得
,使得![]() ,连接
,连接![]() .
.
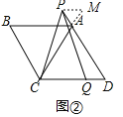
![]() 四边形
四边形![]() 是菱形,
是菱形,![]() ,
,
![]() ,
,![]() 都是等边三角形,
都是等边三角形,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ;
;
③结论:![]() .
.
理由:如图③中,在![]() 上截取
上截取![]() ,连接
,连接![]() .
.
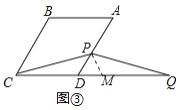
![]() ,
,
![]() ,
,![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.