题目内容
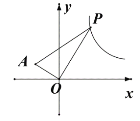
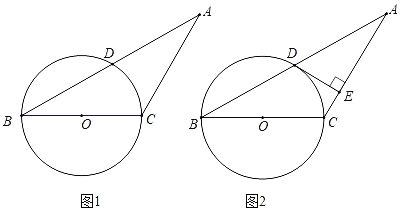
【题目】如图,点![]() 是
是![]() 轴非负半轴上的动点,点
轴非负半轴上的动点,点![]() 坐标为
坐标为![]() ,
,![]() 是线段
是线段![]() 的中点,将点
的中点,将点![]() 绕点
绕点![]() 顺时针方向旋转90°得到点
顺时针方向旋转90°得到点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,过点
,过点![]() 作
作![]() 轴的垂线与直线
轴的垂线与直线![]() 相交于点
相交于点![]() ,连接
,连接![]() ,
,![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
(1)当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(2)设![]() 的面积为
的面积为![]() ,当点
,当点![]() 在线段
在线段![]() 上时,求
上时,求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)当![]() 为何值时,
为何值时,![]() 取得最小值.
取得最小值.
【答案】(1)M(1,2);(2) ![]() ;(3) 当
;(3) 当![]() 时,
时,![]() 取得最小值
取得最小值
【解析】
(1)过![]() 作
作![]() 于
于![]() ,分别求
,分别求![]() 和
和![]() 的长即可;
的长即可;
(2)易证![]() ,可得:
,可得:![]() ,
,![]() ,分别表示
,分别表示![]() 和
和![]() 的长,代入面积公式可求得
的长,代入面积公式可求得![]() 与
与![]() 的关系式;并求其
的关系式;并求其![]() 的取值范围;
的取值范围;
(3)根据(2)得线段长,由勾股定理用![]() 表示
表示![]() 和
和![]() 的长,计算其和,再根据二次根式的意义得出当
的长,计算其和,再根据二次根式的意义得出当![]() 时,值最小.
时,值最小.
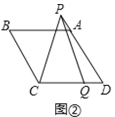
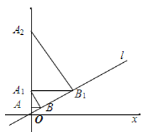
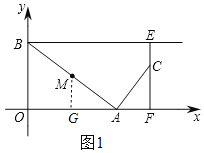
解:(1)如图1,过![]() 作
作![]() 于
于![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,
,
![]() 是
是![]() 的中点,
的中点,
![]() 是
是![]() 的中点,
的中点,
![]() ,
,![]() 是
是![]() 的中位线,
的中位线,
![]() ,
,
![]() ;
;
(2)![]() 点
点![]() 是由点
是由点![]() 绕点
绕点![]() 顺时针方向旋转90°得到的
顺时针方向旋转90°得到的
![]() ,
,![]() ,
,
![]()
∴![]()
![]() ,
,
又![]() ,
,
![]() ,
,![]()
令![]() 得,
得,![]() .
.
![]() ,
,
![]()
![]()
![]()
综上所述,![]() 即为所求.
即为所求.
(3)由(2)得![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由勾股定理得:![]() ,
,
![]() ,
,
![]() ,
,
![]() 当
当![]() 时,
时,![]() 有最小值.
有最小值.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目