题目内容
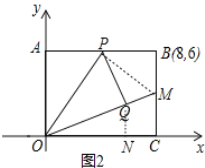
【题目】将矩形纸片OABC放在平面直角坐标系中,0为坐标原点,点A在y轴上,点C在x轴上,点B的坐标是(8,6),点P是边AB上的一个动点,将△OAP沿OP折叠，使点A落在点Q处.
(1)如图①，当点Q恰好落在OB上时.求点p的坐标；
(2)如图②，当点P是AB中点时,直线OQ交BC于M点.
①求证:MB=MQ；②求点Q的坐标.
【答案】（1）P（3，6）；
（2）①证明见解析；②Q（
， 
）
【解析】（1）P（3，6）
（2）⑴证明：连结PM，如图，
∵△OAP沿OP折叠，使点A落在点Q处
∴PQ=PA，∠PQM=OAP=90°
∵点P是AB中点
∴PA=PB，
∴PB=PQ
在Rt△PQM和Rt△PBM中
PB＝PQ
PM＝PM
∴Rt△PQM≌Rt△PBM
∴BM=MQ
⑵Q（
， 
）
练习册系列答案
世纪百通期末金卷系列答案
相关题目
