Question

【题目】 已知，在△ABC中，∠BCA＝90°，AC＝kBC，点D，E分别在边BC，AC上，且AE＝kCD，作线段DF⊥DE，且DE＝kDF，连接EF交AB于点G．

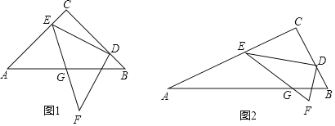
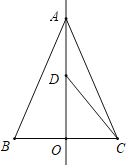
（1）如图1，当k＝1时，求证：①∠CED＝∠BDF，②AG＝GB；

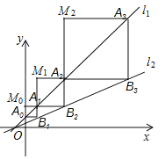
（2）如图2，当k≠1时，猜想的值，并说明理由；

（3）当k＝2，AE＝4BD时，直接写出的值．

Answer 1

【答案】（1）①详见解析；②详见解析；（2），理由详见解析；（3）

【解析】

（1）由同角的余角相等可证，连接BF，易证继而可证，即可得到.

（2）由已知可求，得，由可知，再证，得，结合已知线段关系可知，即可得到.

（3）设BD为x，由k=2、AE=4BD可得AE=2CD=4x，AC=2BC=6x，DE=2DF，通过转化可得CE=CD=2x，进而通过勾股定理可得DE=2DF=2x，即可求出.

解：（1）①∵，，

∴．

∵，，

∴．

②如图，连接BF，

∵，，

∴．

由①知，又∵，

∴．

∴，．

∴．

∴．

∴．

∴，．

∴．

∴．

（2）．理由如下：

如图，连接BF，

∵，，

∴．

∵，，

∴．

∵，，，

∴．

∴．

∴．

∴，．

∴，．

∴．

∴，．

∴．

∴．

∵，，

∴．

∴．

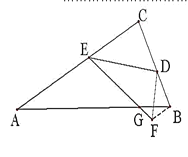
（3）

理由如下：当k=2时，依题意得AE=2CD,AC=2BC,DE=2DF，

又有AE=4BD，

∴CD=2BD，

设BD=x，则CD=2x，BC=3x，AE=4x，AC=6x.

∴CE=2x，

∵∠ACB=90°，

∴DE==2x，

∵DE=2DF，

∴DF=x，

∴