题目内容
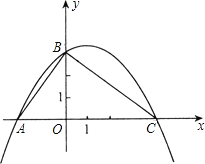
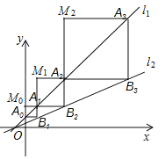
【题目】如图,在平面直角坐标系中,直线l1:y=x+1与y轴交于点A0,过点A0作x轴的平行线交直线l2:y=![]() 点B1,过点B1作y轴的平行线交直线l1于点A1,以A0,B1,A1为顶点构造矩形A0B1A1M0;再过点A1作x轴平行线交直线l2于点B2,过点B2作y轴的平行线交直线l1于点A2,以A1,B2,A2为顶点构造矩形A1B2A2M1;…;照此规律,直至构造矩形AnBn+1An+1Mn,则矩形AnBn+1An+1Mn的周长是_____.
点B1,过点B1作y轴的平行线交直线l1于点A1,以A0,B1,A1为顶点构造矩形A0B1A1M0;再过点A1作x轴平行线交直线l2于点B2,过点B2作y轴的平行线交直线l1于点A2,以A1,B2,A2为顶点构造矩形A1B2A2M1;…;照此规律,直至构造矩形AnBn+1An+1Mn,则矩形AnBn+1An+1Mn的周长是_____.
【答案】2n+2
【解析】
根据直线与x轴的成角和已知,可以判断AnBn+1An+1Mn是正方形,再由直线平行内错角相等得到2A1B1=A1B2,2A2B2=A2B3,…,2AnBn=AnBn+1,可以求得A1B1=1,所以AnBn+1=2n,即可求解.
直线l1:y=x+1与x轴正半轴夹角45°,
∵A0B1∥x轴,A1B2∥x轴,…,AnBn+1∥x轴,
A1B1∥y轴,A2B2∥y轴,…,AnBn∥y轴,
∴四边形A1B2A2M1;…;矩形AnBn+1An+1Mn都是正方形,
B1,B2,…,Bn在直线l2:y=![]() 上,
上,
∴2A1B1=A1B2,2A2B2=A2B3,…,2AnBn=AnBn+1,
∵A0(0,1),
∴B1(1,1),
∴A1B1=1,
∴AnBn+1=2n,
∴AnBn+1An+1Mn的周长2n+2;
故答案为:2n+2

 备战中考寒假系列答案
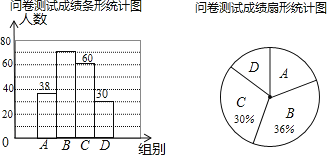
备战中考寒假系列答案【题目】为了了解同学们对垃圾分类知识的了解程度,增强同学们的环保意识某校数学兴趣小组设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试,根据测试成绩分布情况,将测试成绩分成A、B、C、D四组,绘制了如下统计图表
问卷测试成绩分组表
组别 | 分数/分 |
A | 60<x≤70 |
B | 70<x≤80 |
C | 80<x≤90 |
D | 90<x≤100 |
(1)本次抽样调查的样本总量是 ;
(2)样本中,测试成绩在B组的频数是 ,D组的频率是 ;
(3)样本中,这次测试成绩的中位数落在 组;
(4)如果该校共有880名学生,请估计成绩在90<x≤100的学生约有 人.