题目内容
【题目】某工厂计划生产A、B两种产品共60件,需购买甲、乙两种材料,生产一件A产品需甲种材料4千克,乙种材料1千克;生产一件B产品需甲、乙两种材料各3千克,经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂生产的B产品不少于38件且不多于40件,若希望用于购买甲、乙两种材料的资金最少,应如何安排生产?最少购买资金是多少元?
【答案】(1)甲种材料每千克25元,乙种材料每千克35元;(2)生产A产品22件,B产品38件资金最少.最少9810元
【解析】
(1)设甲种材料每千克x元,乙种材料每千克y元,根据“购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元”列出二元一次方程组,求解即可.
(2)设购买材料的资金为w元,生产B产品a件,根据题意列出w关于a的式子,整理可得W是a的一次函数,然后根据a的取值范围以及一次函数的性质可得结果.
解:(1)设甲种材料每千克x元,乙种材料每千克y元,
依题意得:![]() ,
,
解得:![]() ;
;
答:甲种材料每千克25元,乙种材料每千克35元.
(2)设购买材料的资金为w元,生产B产品a件,则生产A产品(60﹣a)件.
依题意得:
![]()
即W是a的一次函数,
∵k=45>0,
∴W随a增大而增大
∵38≤a≤40
∴当a=38时,w=45×38+8100=9810元,购买材料的资金最少;
即生产A产品22件,B产品38件资金最少.最少9810元.

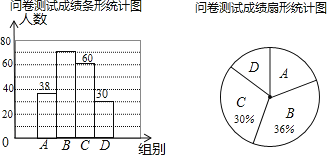
【题目】为了了解同学们对垃圾分类知识的了解程度,增强同学们的环保意识某校数学兴趣小组设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试,根据测试成绩分布情况,将测试成绩分成A、B、C、D四组,绘制了如下统计图表
问卷测试成绩分组表
组别 | 分数/分 |
A | 60<x≤70 |
B | 70<x≤80 |
C | 80<x≤90 |
D | 90<x≤100 |
(1)本次抽样调查的样本总量是 ;
(2)样本中,测试成绩在B组的频数是 ,D组的频率是 ;
(3)样本中,这次测试成绩的中位数落在 组;
(4)如果该校共有880名学生,请估计成绩在90<x≤100的学生约有 人.