题目内容
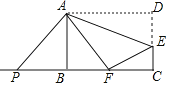
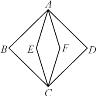
【题目】定义:如图,若菱形AECF与正方形ABCD两个顶点A,C重合,另外两个顶点E,F在正方形ABCD的内部,则称菱形AECF为正方形ABCD的内含菱形.
若正方形的周长为16,其内含菱形边长是整数,则内含菱形的周长为________;
若正方形的面积为18,其内含菱形的面积为6,则内含菱形的边长为________.
【答案】12 ![]()
【解析】
连接AC,BD,AC、BD交于点O,如图,由正方形和菱形的性质可得E、F在BD上,且EF⊥AC,易求得OA的长,在Rt△AOE中,由勾股定理可得OA2+OE2=AE2,由![]() 可得
可得![]() ,然后即可确定整数AE的长,进而可得菱形的周长;由正方形的面积是18可求出其边长,进而可求得AC的长,然后即可求出OE的长,进一步根据勾股定理即可求出菱形的边长.
,然后即可确定整数AE的长,进而可得菱形的周长;由正方形的面积是18可求出其边长,进而可求得AC的长,然后即可求出OE的长,进一步根据勾股定理即可求出菱形的边长.
解:连接AC,BD,AC、BD交于点O,如图,
∵四边形ABCD是正方形,∴AC⊥BD,AC=BD,
∵四边形AECF是菱形,∴E、F在BD上,且EF⊥AC,
∵正方形的周长为16,∴AB=4,
∴2OA2=AB2,即2OA2=16,解得:OA=2![]() ,
,
∴OE<2![]() ,
,
在Rt△AOE中,∵OA2+OE2=AE2,∴8+OE2=AE2,
∵![]() ,∴
,∴![]() ,
,
∵AE是整数,∴AE=3,则内含菱形的周长为12;

若正方形的面积为18,∴AB=3![]() ,
,
∴OA=3,
∵其内含菱形的面积为6,
∴EF=2,∴OE=1,
则内含菱形的边长![]() .
.
故答案为:12;![]() .
.

 阅读快车系列答案
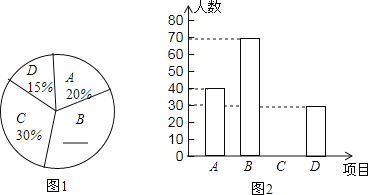
阅读快车系列答案【题目】为了解学生每天的睡眠情况,某初中学校从全校800名学生中随机抽取了40名学生,调查了他们平均每天的睡眠时间(单位:h),统计结果如下:9,8,10.5,7,9,8,10,9.5,8,9,9.5,7.5,9.5,9,8.5,7.5,10,9.5,8,9,7,9.5,8.5,9,7,9,9,7.5,8.5,8.5,9,8,7.5,9.5,10,9.5,8.5,9,8,9.在对这些数据整理后,绘制了如图的统计图表:
睡眠时间分组统计表:
组别 | 睡眠时间分组 | 人数(频数) |
1 | 7≤t<8 | m |
2 | 8≤t<9 | 11 |
3 | 9≤t<10 | n |
4 | 10≤t<11 | 4 |
请根据以上信息,解答下列问题:
(1)m= ,n= ,a= ,b= ;
(2)抽取的这40名学生平均每天睡眠时间的中位数落在 组(填组别);在扇形统计图中,第4组所在扇形的圆心角是 度;
(3)如果按照学校要求,学生平均每天的睡眠时间应不少于9h.请估计该校学生中睡眠时间符合要求的人数.

【题目】疫情无情人有情,爱心捐款传真情,新型冠状病毒感染的肺炎疫情期间,某班学生积极参加献爱心活动,该班50名学生的捐款统计情况如下表:
金额/元 | 5 | 10 | 20 | 50 | 100 |
人数 | 6 | 17 | 14 | 8 | 5 |
则他们捐款金额的众数和中位数分别是( )
A.100,10B.10,20C.17,10D.17,20
【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如下表:
原进价(元/张) | 零售价(元/张) | 成套售价(元/套) | |
餐桌 | a | 380 | 940 |
餐椅 |
| 160 |
已知用600元购进的餐椅数量与用1300元购进的餐桌数量相同.
(1)求表中a的值;
(2)该商场计划购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.若将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售,请问怎样进货,才能获得最大利润?最大利润是多少?