��Ŀ����
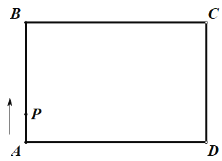
����Ŀ��Ϊ��ά��ÿ��ѧ��ƽ�Ƚ��ܽ�����Ȩ��������Сѧ�������������ͽ���Ƭ��ѧ��ԭ��ʵ��������������������ְ࣬�ְ�ʱ������ѧ��һ��ͬ�ʣ�С���С������Ů�����ھӣ��������챻���ֵ�������ͬһ��Сѧ������ѧУһ�꼶��1�ࡢ2�ࡢ3�ࡢ4��ĸ��࣮�����Ƿְ�ǰ����Ů���ҳ���һ�ζԻ���
С������˵������ϣ�������ֵܷ�ͬһ���࣮��
С������˵�����������ֵܷ�ͬһ���࣬Ҳ���ֲܷ���ͬһ���࣬���������ֵ�ͬһ����Ŀ�������50%����
��������ѧ��֪ʶ����С�������˵���Ƿ���ȷ������ȷ����˵�����ɣ��粻��ȷ�����б�����״ͼ�ķ������С���С���ֵ�ͬһ����ĸ��ʣ�
���𰸡�С���������˵������ȷ��![]()
��������
���������б�����״ͼ���ٸ����б�����״ͼ������⼴�ɣ�
�⣺С���������˵������ȷ��
�б����£�
�� | 1�� | 2�� | 3�� | 4�� |
�� | ||||
1�� | ��1�࣬1�ࣩ | ��1�࣬2�ࣩ | ��1�࣬3�ࣩ | ��1�࣬4�ࣩ |
2�� | ��2�࣬1�ࣩ | ��2�࣬2�ࣩ | ��2�࣬3�ࣩ | ��2�࣬4�ࣩ |
3�� | ��3�࣬1�ࣩ | ��3�࣬2�ࣩ | ��3�࣬3�ࣩ | ��3�࣬4�ࣩ |
4�� | ��4�࣬1�ࣩ | ��4�࣬2�ࣩ | ��4�࣬3�ࣩ | ��4�࣬4�ࣩ |
����״ͼ���ԣ���
���б�������״ͼ����֪һ����16�ֿ��ܳ��ֵĽ������ÿ�ֽ�����ֵĿ�������ͬ������С���С���ֵ�ͬһ����Ľ����4�֣�
���ԣ�![]() ��
��

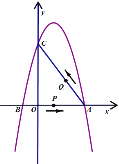
 �������Ͽ��㱾ϵ�д�
�������Ͽ��㱾ϵ�д�����Ŀ����ͼ���ھ���![]() �У�
��![]() ��
��![]() �ӳ����ϵĶ��㣬
�ӳ����ϵĶ��㣬![]() Ϊ
Ϊ![]() ���ϵ�һ�����㣬����
���ϵ�һ�����㣬����![]() ��������
��������![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת
˳ʱ����ת![]() ��������
��������![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��
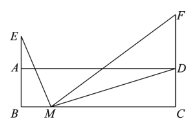
С������ѧϰ�����ľ��飬���߶�![]() �ij���֮��Ĺ�ϵ������̽����
�ij���֮��Ĺ�ϵ������̽����
������С��̽���Ĺ��̣��벹��������
��1�����ڵ�![]() ��
��![]() �ϵIJ�ͬλ�ã���ͼ���������õ����߶�
�ϵIJ�ͬλ�ã���ͼ���������õ����߶�![]() �ij��ȵļ���ֵ�����±���
�ij��ȵļ���ֵ�����±���
�1 | �2 | �3 | �4 | �5 | �6 | �7 | �8 | �9 | |
| 0.00 | 0.53 | 1.00 | 1.69 | 2.17 | 2.96 | 3.46 | 3.79 | 4.00 |
| 0.00 | 1.00 | 1.74 | 2.49 | 2.69 | 2.21 | 1.14 | 0.00 | 1.00 |
| 4.12 | 3.61 | 3.16 | 2.52 | 2.09 | 1.44 | 1.14 | 1.02 | 1.00 |
��![]() �ij������������У�ȷ��_____�ij������Ա�����_____�ij��Ⱥ�_____�ij��ȶ�������Ա����ĺ�����
�ij������������У�ȷ��_____�ij������Ա�����_____�ij��Ⱥ�_____�ij��ȶ�������Ա����ĺ�����
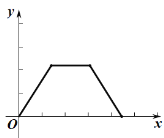
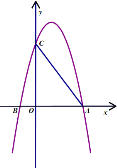
��2����ͬһƽ��ֱ������ϵ![]() �У�������1������ȷ��������������ͼ��
�У�������1������ȷ��������������ͼ��
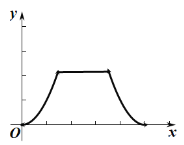
��3����ϻ����ĺ���ͼ������⣺��![]() ʱ��
ʱ��![]() �ij���ԼΪ________
�ij���ԼΪ________![]() ��
��