��Ŀ����
����Ŀ����ͼ��������y=��x2+bx+c����A����1��0����B��3��0�����㣬����y�ύ�ڵ�C����D�������ߵĶ��㣬�����ߵĶԳ���DE��x���ڵ�E������BD��
��1����A��B��C����������ߵĺ�������ʽ��
��2����P���߶�BD��һ�㣬��PE=PCʱ�����P�����ꣻ
��3���ڣ�2���������£�����P��PF��x���ڵ�F��GΪ��������һ���㣬MΪx����һ���㣬NΪֱ��PF��һ���㣬����F��M��GΪ������ı�����������ʱ���������M�����꣮
���𰸡�
��1��
�⣺��������y=��x2+bx+c����A����1��0����B��3��0�����㣬
�� ![]() ��
��
��ã� ![]() ��
��
�ྭ��A��B��C����������ߵĺ�������ʽΪy=��x2+2x+3
��2��
�⣺��ͼ1 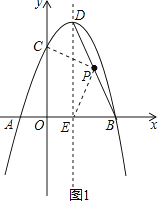 ������PC��PE��
������PC��PE��
x=�� ![]() =��
=�� ![]() =1��
=1��
��x=1ʱ��y=4��
���D��������1��4����
��ֱ��BD�Ľ���ʽΪ��y=mx+n��
�� ![]() ��
��
��ã� ![]() ��
��
��ֱ��BD�Ľ���ʽΪy=��2x+6��
���P��������x����2x+6����
��PC2=x2+��3+2x��6��2��PE2=��x��1��2+����2x+6��2��
��PC=PE��
��x2+��3+2x��6��2=��x��1��2+����2x+6��2��
��ã�x=2��
��y=��2��2+6=2��
���P��������2��2����
��3��
�⣺���M������Ϊ��a��0�������G������Ϊ��a����a2+2a+3����
����F��M��GΪ������ı����������Σ�
��FM=MG����|2��a|=|��a2+2a+3|��
��2��a=��a2+2a+3ʱ��
�����ã�a2��3a��1=0��
��ã�a= ![]() ��
��
��2��a=������a2+2a+3��ʱ��
�����ã�a2��a��5=0��
��ã�a= ![]() ��
��
�൱��F��M��GΪ������ı�����������ʱ����M������Ϊ�� ![]() ��0������
��0������ ![]() ��0������
��0������ ![]() ��0������
��0������ ![]() ��0��
��0��
����������1�����ô���ϵ���������A��B��C����������ߵĺ�������ʽ��
����������2������PC��PE�����ù�ʽ�������D�����꣬���ô���ϵ�������ֱ��BD�Ľ���ʽ�������P������Ϊ��x����2x+6�������ù��ɶ�����ʾ��PC2��PE2 �� ���������г����̣��ⷽ�����x��ֵ�����������P�����ꣻ��
����������3�����M������Ϊ��a��0������ʾ����G�����꣬���������ε������г����̣��ⷽ�̼��ɣ����⿼����Ƕ��κ�����ͼ������ʡ�����ϵ������������ʽ�Լ������ε����ʣ����ն��κ�����ͼ������ʡ�������ô���ϵ�����ǽ���Ĺؼ���
�����㾫�������ö��κ�����ͼ��Ͷ��κ��������ʶ���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪���κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��

 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�