题目内容
【题目】对于一个矩形ABCD及⊙M给出如下定义:在同一平面内,如果矩形ABCD的四个顶点到⊙M上一点的距离相等,那么称这个矩形ABCD是⊙M的“伴侣矩形”.如图,在平面直角坐标系xOy中,直线l:y= ![]() x﹣3交x轴于点M,⊙M的半径为2,矩形ABCD沿直线运动(BD在直线l上),BD=2,AB∥y轴,当矩形ABCD是⊙M的“伴侣矩形”时,点C的坐标为 .
x﹣3交x轴于点M,⊙M的半径为2,矩形ABCD沿直线运动(BD在直线l上),BD=2,AB∥y轴,当矩形ABCD是⊙M的“伴侣矩形”时,点C的坐标为 . 
【答案】( ![]() ﹣
﹣ ![]() ,﹣
,﹣ ![]() )或(
)或( ![]() +
+ ![]() ,
, ![]() )
)
【解析】解:如图所示,矩形在这两个位置时就是⊙M的“伴侣矩形”,根据直线l:y= ![]() x﹣3得:OM=
x﹣3得:OM= ![]() ,ON=3,由勾股定理得:MN=
,ON=3,由勾股定理得:MN= ![]() =2
=2 ![]() ,
,
①矩形在x轴下方时,分别过A、D作两轴的垂线AH、DG,
由cos∠ABD=cos∠ONM= ![]() ,∴
,∴ ![]() =
= ![]() ,AB=
,AB= ![]() ,则AD=1,
,则AD=1,
∵DG∥y轴,
∴△MDG∽△MON,
∴ ![]() ,∴
,∴ ![]() ,∴DG=
,∴DG= ![]() ,∴CG=
,∴CG= ![]() +
+ ![]() =
= ![]() ,同理可得:
,同理可得: ![]() ,∴
,∴ ![]() ,∴DH=
,∴DH= ![]() ,∴C(
,∴C( ![]() ﹣
﹣ ![]() ,﹣
,﹣ ![]() );②矩形在x轴上方时,同理可得:C(
);②矩形在x轴上方时,同理可得:C( ![]()
![]() ,
, ![]() );
);
故答案为:( ![]() ﹣
﹣ ![]() ,﹣
,﹣ ![]() )或(
)或( ![]() +
+ ![]() ,
, ![]() ).
).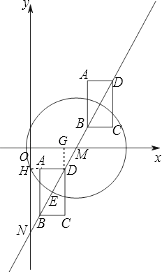
根据“伴侣矩形”的定义可知:圆上的点一定在矩形的对角线交点上,因为只有对角线交点到四个顶点的距离相等,由此画出图形,先求出直线与x轴和y轴两交点的坐标,和矩形的长和宽;
有两种情况:①矩形在x轴下方时,作辅助线构建相似三角形得比例式,分别求出DG和DH的长,从而求出CG的长,根据坐标特点写出点C的坐标;②矩形在x轴上方时,也分别过C、B两点向两坐标轴作垂线,利用平行相似得比例式,求出:C( ![]()
![]() ,
, ![]() ).此题主要考查了圆的综合应用以及相似三角形的性质和矩形等知识,综合性较强,解答本题需要我们熟练各部分的内容,对学生的综合能力要求较高,一定要注意将所学知识贯穿起来.同时,正确理解题意准确画出符合条件的矩形是本题的关键,这就需要熟练掌握矩形的对角线的交点到四个顶点的距离相等.
).此题主要考查了圆的综合应用以及相似三角形的性质和矩形等知识,综合性较强,解答本题需要我们熟练各部分的内容,对学生的综合能力要求较高,一定要注意将所学知识贯穿起来.同时,正确理解题意准确画出符合条件的矩形是本题的关键,这就需要熟练掌握矩形的对角线的交点到四个顶点的距离相等.