题目内容
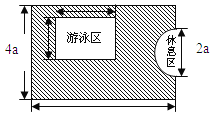
【题目】如图,是一个长方形娱乐场所,其宽是4a米,长是6a米,现要求这个娱乐场拥有一半以上的绿地.小明提供了如图所示的设计方案,其中半圆形休息区和长方形游泳区以外的地方都是绿地,并且半圆形休息区的直径和长方形游泳区的宽都是2a米,游泳区的长3a米.
(1)长方形娱乐场所的面积为 平方米,
休息区的面积为 平方米.
(2)请你判断他的设计方案是否符合娱乐场拥有一半以上的绿地的要求?并说明理由.
(3)若长方形娱乐场所的宽为80米,绿化草地每平方米需要费用20元,求小明设计方案中绿化草地的费用(π取3).
【答案】(1)24a2,![]() ;(2)他的设计方案符合要求,理由见解析;(3)小明设计方案中绿化草地的费用为132000元.
;(2)他的设计方案符合要求,理由见解析;(3)小明设计方案中绿化草地的费用为132000元.
【解析】
(1)根据长方形面积公式和半圆的面积求法列出代数式即可;
(2)求出休息区和游泳区的总面积,然后根据题意判断即可;
(3)根据题意,可以计算出a的值,然后根据绿化草地每平方米需要费用20元,即可求得小明设计方案中绿化草地的费用.
解:(1)由题意可得,
长方形娱乐场所的面积为:6a×4a=24a2,
休息区的面积为:![]() ,
,
故答案为:24a2,![]() ;
;
(2)他的设计方案符合要求,
理由:∵休息区和游泳区总面积为:3a×2a +![]() =6a2+
=6a2+![]() <
<![]() ×24a2,
×24a2,
∴他的设计方案符合要求;
(3)由题意可得,4a=80,解得,a=20,
∴绿化草地的费用为:[24a2(6a2+![]() )]×20=[24×202(6×202+
)]×20=[24×202(6×202+![]() )]×20=132000(元),
)]×20=132000(元),
答:小明设计方案中绿化草地的费用为132000元.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】甲、乙两名同学进入八年级后,某科6次考试成绩如图所示:
平均数 | 方差 | 中位数 | 众数 | |
甲 | 75 | 75 | ||
乙 | 33.3 | 70 |
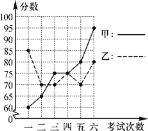
(1)请根据统计图填写上表:
(2)请你分别从以下两个不同的方面对甲、乙两名同学6次考试成绩进行
①从平均数和方差相结合看,你得出什么结论;
②从折线图上两名同学分数的走势上看,你认为反映出什么问题?