题目内容
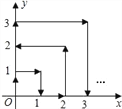
【题目】观察如图所示的图形,回答下列问题:
(1) 图中的点被线段隔开分成四层,第一层有1个点,第二层有3个点,第三层有5个点,第四层有___________个点;
(2) 如果要你继续画下去,那么第五层有________点, 第10层有_________点;
(3) 某一层上有77个点,你可知道这是第_________层;
(4) 第一层与第二层的和是__________,前三层的和是_________,前四层和为____________,
你有没有发现什么规律?
根据你的推测,前一百层的和是___________.

【答案】 7 9 19 39 4 9 16 10000
【解析】
(1)由图中信息可知第4层有7个点;
(2)观察图形中各层点的个数可知,从第一层到第n层点的个数依次是从1开始的连续奇数1、3、5、……,由此可知第n层的点的个数为:(2n-1)个,从而可计算出第五层和第十层的点的个数;
(3)根据(2)中所得结论可得2n-1=77,解此方程即可求得对应的n的值;
(4)由图中信息可得第一层点的个数和第二层点的个数的和为4,前三层点的个数之和为9,前四层点的个数之和为16;由此可得规律为:前n层的点的个数之和为![]() ;由此可得前100层的点的个数之和为:
;由此可得前100层的点的个数之和为:![]() 个.
个.
(1)如图所示:第四层有7个点;
(2)∵第一层有1个点,第二层有3个点,第三层有5个点,第四层有7个点,
∴从第一层到第n层点的个数依次是从1开始的连续奇数1、3、5、……,由此可知第n层的点的个数为:(2n-1)个,
∴如果继续画下去,那么第五层有9个点,第十层有19个点;
(3)某一层上有77个点,即:2n-1=77,解得:n=39,
∴这是第三十九层;
(4)∵第一层与第二层点的个数之和是4=22,前三层点的个数的和是9=32,前四层点的个数的和是16=42,…,
由此可得:前n层的点的个数的和是n2,
∴前一百层的点的个数的和是1002=10000.

【题目】去学校食堂就餐,经常会在一个买菜窗口前等待,经调查发现,同学的舒适度指数y与等时间x(分)之间满足反比例函数关系,如下表:
等待时间x | 1 | 2 | 5 | 10 | 20 |
舒适度指数y | 100 | 50 | 20 | 10 | 5 |
已知学生等待时间不超过30分钟
(1)求y与x的函数关系式,并写出自变量x的取值范围.
(2)若等待时间8分钟时,求舒适度的值;
(3)舒适度指数不低于10时,同学才会感到舒适.请说明,作为食堂的管理员,让每个在窗口买菜的同学最多等待多少时间?