题目内容
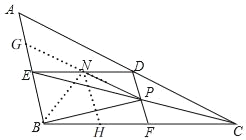
【题目】如图,在△ABC中,CE平分∠ACB交AB于E点,DE∥BC,DF∥AB.
(1)若∠BCE=25°,请求出∠ADE的度数;
(2)已知:BF=2BE,DF交CE于P点,连结BP,AB⊥BP.
①猜想:△CDF的边DF与CD的数量关系,并说明理由;
②取DE的中点N,连结NP.求证:∠ENP=3∠DPN.
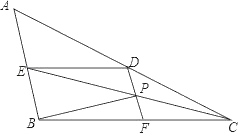
【答案】(1)∠ADE=50°;(2)①CD=2DF;见解析;②见解析.
【解析】
(1)利用角平分线得出∠ACB=2∠BCE=50°,再利用两直线平行,同位角相等即可得出结论;
(2)先判断出四边形BEDF是平行四边形,进而得出DE=2DF,再利用角平分线及平行线得出DE=CD,即可得出结论;
(3)先利用倍长中线法得出NG=NP,∠EGN=∠DPN,再用直角三角形的中线得出∠EGN=∠EBN,再构造出菱形判断出∠BEN=∠BHN,即可得出结。
(1)∵CE平分∠ACB交AB于E点,
∴∠ACB=2∠BCE,
∵∠BCE=25°,
∴∠ACB=50°,
∵DE∥BC,
∴∠ADE=∠ACB=50°;
(2)①∵DE∥BC,DF∥AB,
∴四边形BEDF是平行四边形,
∴DE=BF,DF=BE,
∵BF=2BE,
∴DE=2DF,
∵CE平分∠ACB交AB于E点,
∴∠BCE=∠ACE,
∵DE∥BC,
∴∠DEC=∠BCE,
∴∠DEC=∠DCE,
∴CD=DE,
∵DE=2DF,
∴CD=2DF;
(3)如图,
延长PN交AB于G,
∵DF∥AB,
∴∠EGN=∠DPN,
∵∠ENG=∠DNP,
∵点N是DE中点,
∴EN=DN,
∴△ENG≌△DNP(AAS),
∴∠EGN=∠DPN,GN=PN,
∵AB⊥BP,
∴∠ABP=90°,
∴BN=GN,
∴∠EGN=∠EBN,
∵DE=2EN,DE=2BE,
∴EN=BE,
∴∠ENB=∠EBN=∠EGN=∠DPN,
过点N作NH∥BE交BC于H,
∵BE∥DF,
∴NH∥DF,
∴∠PNH=∠DPN,
∵EN∥BH,NH∥BE,
∴四边形BENH是平行四边形,
∵BE=EN,
∴BENH是菱形,
∵BE是菱形对角线,
∴∠BNH=∠BNE=DPN,
∴∠ENP=∠BNE+∠BNH+∠PNH=∠DPN+∠DPN+∠DPN=3∠DPN.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案