题目内容
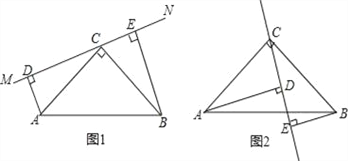
【题目】如图(1)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.求证:
(1)△ADC≌△CEB;
(2)DE=AD+BE.
(3)当直线MN绕点C旋转到图(2)的位置时,DE、AD、BE又怎样的关系?并加以证明.
【答案】证明见解析.
【解析】试题分析:(1)由AAS可证明△ADC≌△CEB;
(2)再利用线段的和差可证得结论;
(3)同(2)的方法可证得结论.
试题解析:(1)证明:∵∠ACB=90°,∴∠ACD+∠BCE=90°,而AD⊥MN于D,BE⊥MN于E,∴∠ADC=∠CEB=90°,∠BCE+∠CBE=90°,∴∠ACD=∠CBE.
在△ADC和△CEB中,∵∠ADC=∠CEB,∠ACD=∠CBE,AC=BC,∴△ADC≌△CEB(AAS);
(2)∵△ADC≌△CEB,∴AD=CE,DC=BE,∴DE=DC+CE=BE+AD;
(3)解:DE=AD﹣BE.理由如下:
在△ADC和△CEB中,∵∠ADC=∠CEB,∠ACD=∠CBE,AC=BC,∴△ADC≌△CEB(AAS),∴AD=CE,DC=BE,∴DE=CE﹣CD=AD﹣BE.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目

