Question

【题目】如图，一次函数y=k1x+b（k1≠0）与反比例函数y=（k2≠0）（x＞0）的图象交于A（1，6），B（a，3）两点，

（1）分别求出一次函数与反比例函数的解析式；

（2）直接写出k1x+b﹣＞0时x（x＞0）的取值范围；

（3）如图，等腰梯形OBCD中，BC∥OD，OB=CD，OD边在x轴上，过点C作CE⊥OD于点E，CE和反比例函数图象交于点P，当梯形OBCD的面积为12时，请判断PC和PE的大小关系，并说明理由．

Answer 1

【答案】(1) 一次函数解析式为：y=﹣3x+9；反比例函数解析式为：y=；（2）1＜x＜2；（3）PC=PE，理由见解析.

【解析】

试题分析：（1）由反比例函数y=（k2≠0）（x＞0）的图象过A（1，6），B（a，3）两点，利用待定系数法即可求得反比例函数的解析式与点B的坐标，然后由y=k1x+b过A（1，6），B（2，3），利用待定系数法求得一次函数的解析式；

（2）结合图象，即可求得k1x+b﹣＞0时x（x＞0）的取值范围；

（3）首先过点B作BF⊥OD于点F，易证得Rt△OBF≌Rt△DCE（HL），即可得OF=DE，然后设C（a，3），由梯形OBCD的面积为12，即可求得a的值，继而求得线段PC与PE的长，则可证得结论．

试题解析：（1）∵y=过A（1，6），B（a，3），

∴6=，3=，

∴k2=6，a=2，

∴反比例函数解析式为：y=，B（2，3），

∵y=k1x+b过A（1，6），B（2，3），

∴，

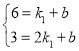解得：．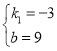

∴一次函数解析式为：y=﹣3x+9；

（2）由图象得：k1x+b﹣＞0时，x（x＞0）的取值范围为：1＜x＜2；

（3）PC=PE，理由如下：

过点B作BF⊥OD于点F，

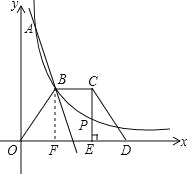
∵四边形OBCD是等腰梯形，BC∥OD，CE⊥OD，

∴OB=CD，BF=CE，

在Rt△OBF和Rt△DCE中，

，

∴Rt△OBF≌Rt△DCE（HL），

∴OF=DE，

∵B（2，3），

∴OF=DE=2，BF=3，

设C（a，3），

∴BC=a﹣2，OD=a+2，

∵梯形OBCD的面积为12，

∴（a﹣2+a+2）×3=12，

解得：a=4，

∴C（4，3），

∴xP=4，

∴yP=，

∴P（4，），

∵C（4，3），E（4，0），

∴PC=3﹣=，

PE=﹣0=，

∴PC=PE．