Question

【题目】已知函数f（x）=ax2﹣（2a﹣1）x﹣lnx（a为常数，a≠0）． （Ⅰ）当a＜0时，求函数f（x）在区间[1，2]上的最大值；
（Ⅱ）记函数f（x）图象为曲线C，设点A（x1 ， y1），B（x2 ， y2）是曲线C上不同的两点，点M为线段AB的中点，过点M作x轴的垂线交曲线C于点N．判断曲线C在点N处的切线是否平行于直线AB？并说明理由．

Answer 1

【答案】解：（Ⅰ）f′（x）= ， 当a＜0时，由f′（x）=0，得x1=﹣ ，x2=1，又x∈[1，2]，则有如下分类：
①当﹣ ≥2，即﹣ ≤a＜0时，f（x）在[1，2]上是增函数，
所以f（x）max=f（2）=2﹣ln2．
②当1＜﹣ ＜2，即﹣ ＜a＜﹣ 时，f（x）在[1，﹣ ）上是增函数，在（﹣ ，2]上是减函数，
所以f（x）max=f（﹣ ）=1﹣ +ln（﹣2a）．
③当﹣ ≤1，即a≤﹣ 时，f（x）在[1，2]上是减函数，
所以f（x）max=f（1）=1﹣a．
综上，函数f（x）在[1，2]上的最大值为：
f（x）max= ；
（Ⅱ）设M（x0 ， y0），则点N的横坐标为x0= ，
直线AB的斜率k1= = [a（x12﹣x22）+（1﹣2a）（x1﹣x2）+lnx2﹣lnx1]
=a（x1+x2）+（1﹣2a）+ ，
C在点N处的切线斜率
k2=f′（x0）=a（x1+x2）+（1﹣2a）﹣ ，
假设曲线C在点N处的切线平行于直线AB，则k1=k2 ，
即 =﹣ ，所以ln = ，
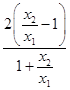不妨设x1＜x2 ， ln =t＞1，则lnt= ，
令g（t）=lnt﹣ ，（t＞1），g′（t）= ＞0，
所以g（t）在（1，+∞）上是增函数，又g（1）=0，
所以g（t）＞0，即lnt= 不成立，
所以曲线C在点N处的切线不平行于直线AB．
【解析】（Ⅰ）求出函数f（x）的导数，通过讨论a的范围，求出函数f（x）的单调区间，从而求出f（x）的最大值即可；（Ⅱ）设出M的坐标，分别求出直线AB的斜率k1 ， C在点N处的切线斜率k2 ， 由k1=k2 ， 得到即 =﹣ ，得出矛盾．
【考点精析】本题主要考查了函数的最大(小)值与导数的相关知识点，需要掌握求函数在上的最大值与最小值的步骤：（1）求函数在内的极值；（2）将函数的各极值与端点处的函数值，比较，其中最大的是一个最大值，最小的是最小值才能正确解答此题．