Question

【题目】已知函数f（x）=x3+ax2+bx有两个极值点x1、x2 ， 且x1＜x2 ， 若x1+2x0=3x2 ， 函数g（x）=f（x）﹣f（x0），则g（x）（ ）
A.恰有一个零点
B.恰有两个零点
C.恰有三个零点
D.至多两个零点

Answer 1

【答案】B
【解析】解：f（x）=x3+ax2+bx，求导，f′（x）=3x2+2ax+b，由函数f（x）有两个极值点x1、x2 ， 则x1、x2是方程3x2+2ax+b=0的两个根，则x1+x2=﹣ ，x1x2= ，
∴a=﹣ ，①
由x1+2x0=3x2 ， 则x0= =x2+ ＞x2 ，
由函数图象可知：令f（x1）=f（x）的另一个解为m，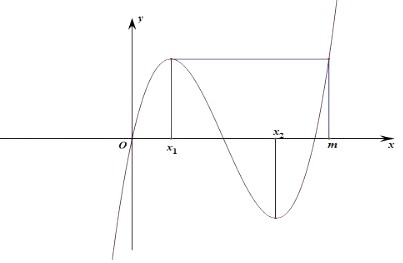

则x3+ax2+bx﹣f（x1）=（x﹣x1）2（x﹣m），
则 ，则m=﹣a﹣2x1 ，
将①代入②整理得：m= ﹣2x1= =x0 ， ∴f（x）=f（m）=f（x0），
∴g（x）只有两个零点，即x0和m，
故选：B．
由题意可知：x1、x2是方程3x2+2ax+b=0的两个根，由韦达定理可知：x1+x2=﹣ ，x1x2= ，由x1+2x0=3x2 ， x0= ＞0，令f（x1）=f（x）的另一个解为m，即可求得m=﹣a﹣2x1 ， 则f（x）=f（m）=f（x0），