��Ŀ����
����Ŀ����ͼ����������ABCD�У�AB=4��P��BC����һ���㣨����B��C���㣩������ABP��ֱ��AP���ۣ���B���ڵ�E������CD����һ��M��ʹ�ý���CMP��ֱ��MP���ۺ�C����ֱ��PE�ϵĵ�F����ֱ��PE��CD�ڵ�N������MA��NA��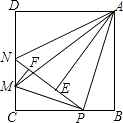
��1�����֣�
��CMP�͡�BPA�Ƿ����ƣ������Ƹ���֤������������˵�����ɣ�
��2��˼����
�߶�AM�Ƿ������Сֵ����������������Сֵ���������ڣ�˵�����ɣ�
��3��̽����
����ABP�ա�ADNʱ����BP��ֵ�Ƕ��٣�
���𰸡�
��1��
�ߡ�APB=��APE����MPC=��MPN����CPN+��NPB=180�㣬
��2��NPM+2��APE=180�㣬
���MPN+��APE=90�㣬
���APM=90�㣬
�ߡ�CPM+��APB=90�㣬��APB+��PAB=90�㣬
���CPM=��PAB��
�֡ߡ�C=��B=90�㣬
���CMP�ס�BPA��
��2��
��PB=x����CP=4��x��
�ߡ�CMP�ס�BPA��
�� ![]() ��
��
��CM= ![]() x��4��x����
x��4��x����
��ͼ1��ʾ����MG��AB��G��
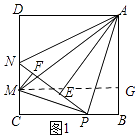
��AM= ![]() =
= ![]() ��
��
��AG��Сֵʱ��AM��С��
��AG=AB��BG=AB��CM=4�� ![]() x��4��x��=
x��4��x��= ![]() ��x��2��2+3��
��x��2��2+3��
��x=2ʱ��AG��Сֵ=3��
��AM����Сֵ= ![]() =5��
=5��
��3��
�ߡ�ABP�ա�ADN��
���PAB=��DAN��AP=AN��
�֡ߡ�PAB=��EAP����AEP=��B=90�㣬
���EAP=��EAN��
���PAB=��DAN=��EAP=��EAN=22.5�㣮
��ͼ2����AB��ȡһ��Kʹ��AK=PK����PB=z��
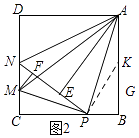
���KPA=��KAP=22.5�㣬
�ߡ�PKB=��KPA+��KAP=45�㣬
���BPK=��BKP=45�㣬
��PB=BK=z��AK=PK= ![]() z��
z��
��z+ ![]() z=4��
z=4��
��z=4 ![]() ��4��
��4��
��PB=4 ![]() ��4��
��4��
�����������֣���֤����MPA=90�㣬Ȼ������ͬ�ǵ������ȿ�֤����CPM=��PAB�����������C=��B=90�㣬��֤�������������ƣ�
˼������PB=x����CP=4��x���������������ε����ʿɵõ�CM= ![]() x��4��x������MG��AB��G�����ݹ��ɶ����ɵõ�AM=
x��4��x������MG��AB��G�����ݹ��ɶ����ɵõ�AM= ![]() ����AG��Сֵʱ��AM��С��Ȼ����AG=AB��BG=AB��CM�õ�AG��x�ĺ�����ϵ�����ݶ��κ��������ʿ���õ�x=2ʱ��AG��Сֵ=3��
����AG��Сֵʱ��AM��С��Ȼ����AG=AB��BG=AB��CM�õ�AG��x�ĺ�����ϵ�����ݶ��κ��������ʿ���õ�x=2ʱ��AG��Сֵ=3��
̽��������ȫ�������ε����ʺͷ��۵����ʿɵõ���PAB=��DAN=��EAP=��EAN=22.5�㣬��AB��ȡһ��Kʹ��AK=PK����PB=z��Ȼ���֤����BPKΪ����ֱ�������Σ��ʴ˵õ�PB=BK=z��AK=PK= ![]() z���������AK+BK=4�г�����z�ķ�����⼴�ɣ�
z���������AK+BK=4�г�����z�ķ�����⼴�ɣ�
�����㾫����ͨ������������������ε��ж������ʣ��������������ε�һ�ж�Ӧ�߶�(��Ӧ�ߡ���Ӧ���ߡ���Ӧ��ƽ���ߡ����Բ�뾶������Բ�뾶�ȣ��ıȵ������Ʊȣ������������ܳ��ıȵ������Ʊȣ���������������ıȵ������Ʊȵ�ƽ�������Խ����⣮

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�