题目内容
【题目】定义：若两个椭圆的离心率相等，则称两个椭圆是“相似”的． 如图，椭圆C1与椭圆C2是相似的两个椭圆，并且相交于上下两个顶点．椭圆C1： 
的长轴长是4，椭圆C2： 
短轴长是1，点F1 ， F2分别是椭圆C1的左焦点与右焦点，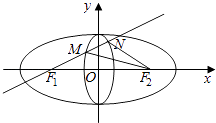 
（Ⅰ）求椭圆C1 ， C2的方程；
（Ⅱ）过F1的直线交椭圆C2于点M，N，求△F2MN面积的最大值．
【答案】解：（Ⅰ）设椭圆C1的半焦距为c，椭圆C2的半焦距为c'．由已知a=2，b=m， 
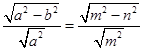． ∵椭圆C1与椭圆C2的离心率相等，即 
，
∴ 
，即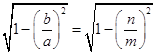 
∴ 
，即bm=b2=an=1，∴b=m=1，
∴椭圆C1的方程是 
，椭圆C2的方程是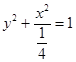 
；
（Ⅱ）显然直线的斜率不为0，故可设直线的方程为： 
．
联立：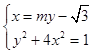 
，得 
，即 
，
∴△=192m2﹣44（1+4m2）=16m2﹣44＞0，设M（x1 ， y1），N（x2 ， y2），
则 
， 
，∴ 
，
△F2MN的高即为点F2到直线 
的距离h=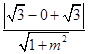 
= 
，
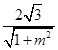∴△F2MN的面积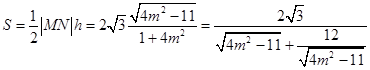 
，
∵ 
，等号成立当且仅当 
，即 
时，
∴ 
，即△F2MN的面积的最大值为 
．
【解析】（Ⅰ）设椭圆C1的半焦距为c，椭圆C2的半焦距为c'，易知a=2，b=m，n= 
，根据椭圆C1与椭圆C2的离心率相等，可得关于a，b，m，n的方程，解出即可；（Ⅱ）由题意可设直线的方程为： 
．与椭圆C2的方程联立消掉x得y的二次方程，则△＞0，由弦长公式可表示出|MN|，由点到直线的距离公式可表示出△F2MN的高h，则△F2MN的面积S= 
，变形后运用基本不等式即可求得S的最大值；
【考点精析】通过灵活运用椭圆的标准方程，掌握椭圆标准方程焦点在x轴：
，焦点在y轴：
即可以解答此题．
【题目】2017年是某市大力推进居民生活垃圾分类的关键一年，有关部门为宣传垃圾分类知识，面向该市市民进行了一次“垃圾分类知识”的网络问卷调查，每位市民仅有一次参与机会，通过抽样，得到参与问卷调查中的1000人的得分数据，其频率分布直方图如图所示： 
（1）由频率分布直方图可以认为，此次问卷调查的得分Z服从正态分布N（μ，210），μ近似为这1000人得分的平均值（同一组数据用该区间的中点值作代表），利用该正态分布，求P（50.5＜Z＜94）．
（2）在（1）的条件下，有关部门为此次参加问卷调查的市民制定如下奖励方案： ①得分不低于μ可获赠2次随机话费，得分低于μ则只有1次；
②每次赠送的随机话费和对应概率如下：
赠送话费（单位：元） | 10 | 20 |
概率 |
|
|
现有一位市民要参加此次问卷调查，记X（单位：元）为该市民参加问卷调查获赠的话费，求X的分布列．
附： 
≈14.5
若Z～N（μ，δ2），则P（μ﹣δ＜Z＜μ+δ）=0.6826，P（μ﹣2δ＜Z＜μ+2δ）=0.9544．
