题目内容
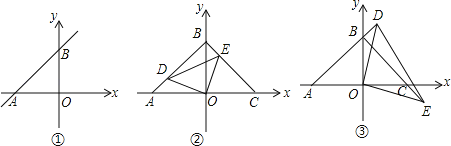
【题目】如图①，直线AB与x轴负半轴、y轴正半轴分别交于A、B两点，OA、OB的长度分别为a和b，且满足a2﹣2ab+b2=0．
（1）判断△AOB的形状；
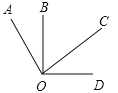
（2）如图②，△COB和△AOB关于y轴对称，D点在AB上，点E在BC上，且AD=BE，试问：线段OD、OE是否存在某种确定的数量关系和位置关系？写出你的结论并证明；
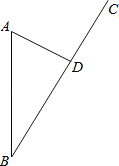
（3）将（2）中∠DOE绕点O旋转，使D、E分别落在AB，BC延长线上（如图③），∠BDE与∠COE有何关系？直接说出结论，不必说明理由．
【答案】（1）△AOB为等腰直角三角形；（2）OD⊥OE；（3）∠BDE与∠COE互余．
【解析】
试题分析：（1）根据a2﹣2ab+b2=0，可得a=b，又由∠AOB=90°，所以可得出△AOB的形状；
（2）OD=OE，OD⊥OE，通过证明△OAD≌△OBE可以得证；
（3）由∠DEB+∠BEO=45°，∠ACB=∠COE+∠BEO=45°，得出∠DEB=∠COE，根据三角形外角的性质得出∠ABC=∠BDE+∠DEB=90°，从而得出∠BDE+∠COE=90°，所以∠BDE与∠COE互余．
解：（1）∵a2﹣2ab+b2=0．
∴（a﹣b）2=0，
∴a=b，
又∵∠AOB=90°，
∴△AOB为等腰直角三角形；
（2）OD=OE，OD⊥OE，理由如下：
如图 ②，∵△AOB为等腰直角三角形，
∴AB=BC，
∵BO⊥AC，
∴∠DAO=∠EBO=45°，BO=AO，
在△OAD和△OBE中，
，
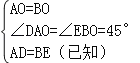△OAD≌△OBE（SAS），
∴OD=OE，∠AOD=∠BOE，
∵∠AOD+∠DOB=90°，
∴∠DOB+∠BOE=90°，
∴OD⊥OE；
（3）∠BDE与∠COE互余，理由如下：
如图③，∵OD=OE，OD⊥OE，
∴△DOE是等腰直角三角形，
∴∠DEO=45°，
∴∠DEB+∠BEO=45°，
∵∠ACB=∠COE+∠BEO=45°，
∴∠DEB=∠COE，
∵∠ABC=∠BDE+∠DEB=90°，
∴∠BDE+∠COE=90°
∴∠BDE与∠COE互余．
