Question

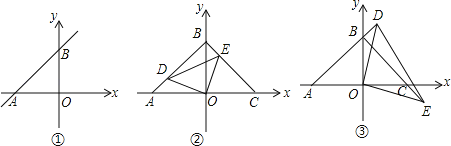
【题目】如图，点B、C、E在同一条直线上，△ABC与△CDE都是等边三角形，则下列结论不一定成立的是（ ）

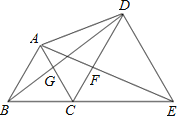
A．△ACE≌△BCD B．△BGC≌△AFC

C．△DCG≌△ECF D．△ADB≌△CEA

Answer 1

【答案】D

【解析】

试题分析：首先根据角间的位置及大小关系证明∠BCD=∠ACE，再根据边角边定理，证明△BCE≌△ACD；由△BCE≌△ACD可得到∠DBC=∠CAE，再加上条件AC=BC，∠ACB=∠ACD=60°，可证出△BGC≌△AFC，再根据△BCD≌△ACE，可得∠CDB=∠CEA，再加上条件CE=CD，∠ACD=∠DCE=60°，又可证出△DCG≌△ECF，利用排除法可得到答案．

解：∵△ABC和△CDE都是等边三角形，

∴BC=AC，CE=CD，∠BCA=∠ECD=60°，

∴∠BCA+∠ACD=∠ECD+∠ACD，

即∠BCD=∠ACE，

∴在△BCD和△ACE中 ，

∴△BCD≌△ACE（SAS），

故A成立，

∴∠DBC=∠CAE，

∵∠BCA=∠ECD=60°，

∴∠ACD=60°，

在△BGC和△AFC中，

∴△BGC≌△AFC，

故B成立，

∵△BCD≌△ACE，

∴∠CDB=∠CEA，

在△DCG和△ECF中，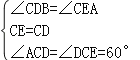

∴△DCG≌△ECF，

故C成立，

故选：D．