题目内容
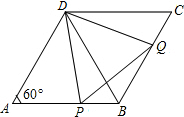 如图,在菱形ABCD中,∠A=60°,点P、Q分别在边AB、BC上,且AP=BQ.
如图,在菱形ABCD中,∠A=60°,点P、Q分别在边AB、BC上,且AP=BQ.求证:△BDQ≌△ADP.
分析:由在菱形ABCD中,∠A=60°,易得△ABD和△BDC是等边三角形,即可得∠DBQ=∠A=60°,AD=DB,然后由SAS判定:△BDQ≌△ADP.
解答:证明:∵四边形ABCD是菱形,且∠A=60°,
∴AD=AB=BC=CD,∠C=∠A=60°,
∴△ABD和△BDC是等边三角形,
∴∠DBQ=∠A=60°,AD=DB,
在△BDQ和△ADP中,
,
∴△BDQ≌△ADP(SAS).
∴AD=AB=BC=CD,∠C=∠A=60°,
∴△ABD和△BDC是等边三角形,
∴∠DBQ=∠A=60°,AD=DB,
在△BDQ和△ADP中,
|
∴△BDQ≌△ADP(SAS).
点评:此题考查了菱形的性质、等边三角形的判定与性质以及全等三角形的判定与性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
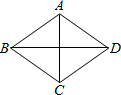 如图:在菱形ABCD中,AC=6,BD=8,则菱形的边长为( )
如图:在菱形ABCD中,AC=6,BD=8,则菱形的边长为( )| A、5 | B、10 | C、6 | D、8 |
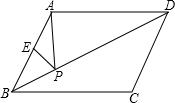
 ME交射线CD于点N,连接MD、AN.
ME交射线CD于点N,连接MD、AN. (2013•攀枝花)如图,在菱形ABCD中,DE⊥AB于点E,cosA=
(2013•攀枝花)如图,在菱形ABCD中,DE⊥AB于点E,cosA= 如图,在菱形ABCD中,AE⊥BC,垂足为F,EC=1,∠B=30°,求菱形ABCD的周长.
如图,在菱形ABCD中,AE⊥BC,垂足为F,EC=1,∠B=30°,求菱形ABCD的周长.