Question

【题目】我们知道，三角形三个内角平分线的交点叫做三角形的内心，已知点I为△ABC的内心．

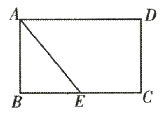
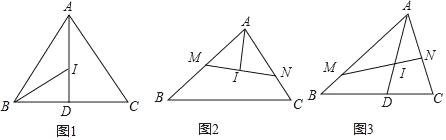
（1）如图1，连接AI并延长交BC于点D，若AB=AC=3，BC=2，求ID的长；

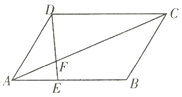
（2）如图2，过点I作直线交AB于点M，交AC于点N．

①若MN⊥AI，求证：MI2=BMCN；

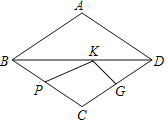
②如图3，AI交BC于点D，若∠BAC=60°，AI=4，求的值．

Answer 1

【答案】（1）；（2）见解析；（3）．

【解析】

（1）如图1中，作IE⊥AB于E．设ID=x．由△BEI≌△BDI，可得ID=IE=x，BD=BE=1，AE=2，在Rt△AEI中，根据AE2+EI2=AI2，可得解方程即可；
（2）如图2中，连接BI、CI．首先证明△AMI≌△ANI（ASA），再证明△BMI∽△INC，可得，推出NI2=BMCN，由此即可解决问题；
（3）过点N作NG∥AD交MA的延长线于G．由∠ANG=∠AGN=30°，推出AN=AG，由AI∥NG，推出，可得即可推出

（1）如图1中，作IE⊥AB于E．设ID=x．

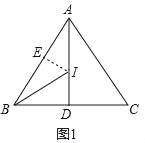
∵AB=AC=3，AI平分∠BAC，

∴AD⊥BC，BD=CD=1，

在Rt△ABD中，

∵∠EBI=∠DBI，∠BEI=∠BDI=90°，BI=BI，

∴△BEI≌△BDI，

∴ID=IE=x，BD=BE=1，AE=2，

在Rt△AEI中，∵AE2+EI2=AI2，

∴

∴

∴

（2）如图2中，连接BI、CI．

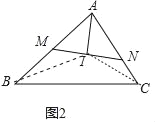
∵I是内心，

∴∠MAI=∠NAI，

∵AI⊥MN，

∴∠AIM=∠AIN=90°，

∵AI=AI，

∴△AMI≌△ANI（ASA），

∴∠AMN=∠ANM，

∴∠BMI=∠CNI，

设∠BAI=∠CAI=α，∠ACI=∠BCI=β，

∴∠NIC=90°﹣α﹣β，

∵∠ABC=180°﹣2α﹣2β，

∴∠MBI=90°﹣α﹣β，

∴∠MBI=∠NIC，

∴△BMI∽△INC，

∴

∴NI2=BMCN，

∵NI=MI，

∴MI2=BMCN．

（3）过点N作NG∥AD交MA的延长线于G．

∴∠ANG=∠AGN=30°，

∴AN=AG，

∵AI∥NG，

∴

∴

∴