题目内容
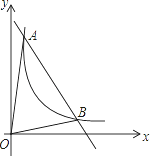
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)的图象交于A(m,6),B(3,n)两点
(x>0)的图象交于A(m,6),B(3,n)两点
(1)求一次函数的解析式;
(2)根据图象直接写出使kx+b<![]() 成立的x的取值范围;
成立的x的取值范围;
(3)求△AOB的面积.
【答案】(1)y=﹣2x+8;(2)0<x<1或x>3;(3)8.
【解析】试题分析:(1)、首先根据反比例函数的解析式得出点A和点B的坐标,然后根据待定系数法求出一次函数的解析式;(2)、根据函数图形得出答案;(3)、分别过点A、B作AE⊥x轴,BC⊥x轴,垂足分别是E、C点.直线AB交x轴于D点,将△OAB的面积转化成△OAD的面积减去△OBD的面积.
试题解析:(1)、∵点A(m,6),B(3,n)两点在反比例函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴m=1,n=2, 即A(1,6),B(3,2). 又∵点A(m,6),B(3,n)两点在一次函数y=kx+b的图象上,
∴![]() . 解得
. 解得![]() , 则该一次函数的解析式为:y=﹣2x+3;
, 则该一次函数的解析式为:y=﹣2x+3;
(2)、根据图象可知使kx+b<![]() 成立的x的取值范围是0<x<1或x>2;
成立的x的取值范围是0<x<1或x>2;
(3)、分别过点A、B作AE⊥x轴,BC⊥x轴,垂足分别是E、C点.直线AB交x轴于D点.
令﹣2x+8=0,得x=4,即D(4,0).
∵A(1,6),B(3,2), 则![]() =4×6÷2-4×2÷2=12-4=8
=4×6÷2-4×2÷2=12-4=8

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
相关题目