Question

【题目】如图，正方形纸片ABCD的边长为12，E是边CD上一点，连接AE，折叠该纸片，使点A落在AE上的G点，并使折痕经过点B，得到折痕BF，点F在AD上，若DE=5，则GE的为_______________.

Answer 1

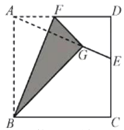
【答案】

【解析】

设BF和AG交于点O，根据折叠的性质可得：FA=FG，BA=BG，从而证出BF垂直平分AG，根据正方形的性质和全等三角形的判定可证出：△DAE≌△ABF，从而求出DE=AF=5，然后利用相似三角形的判定可得：△OAF∽△DAE，列出比例式即可求出AO和OG，从而求出GE.

解：设BF和AG交于点O

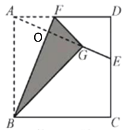
由折叠的性质可得：FA=FG，BA=BG

∴点F、B都在AG的中垂线上

根据两点确定一条直线

∴BF垂直平分AG

即AO=OG，∠AOB=∠AOF=90°

∴∠ABF＋∠BAE=90°

∵四边形ABCD是正方形

∴AD=AB=12，∠D=∠FAB=90°

∴∠DAE＋∠BAE=90°，根据勾股定理可得：AE=

∴∠DAE=∠ABF

在△DAE和△ABF中

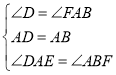
∴△DAE≌△ABF

∴DE=AF=5

∵∠OAF=∠DAE

∴△OAF∽△DAE

∴

即：

解得：

∴

∴GE=AE－OG－OA=

故答案为：.