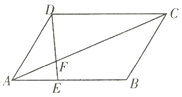
题目内容
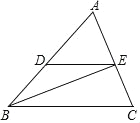
【题目】如图所示,在![]() 中,
中,![]() ,联结
,联结![]() 交
交![]() 于点
于点![]() .
.
(1)求![]() 与
与![]() 的周长比;
的周长比;
(2)如果![]() ,求
,求![]() 与
与![]() .
.
【答案】(1)1:3 (2)54![]() ;144
;144![]()
【解析】
(1)易证△AEF∽△CDF,由相似三角形的性质:周长之比等于相似比即可求出△AEF与△CDF的周长的比;
(2)由(1)可知△AEF∽△CDF,由相似三角形的性质:面积之比等于相似比的平方即可求出S△CDF,再根据三角形面积关系求出S△ADF即可解决问题.
解:(1)∵AE:EB=1:2,
∴AE:AB=1:3,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴△AEF∽△CDF,
∴C△AEF:C△CDF=AE:CD=AE:AB=1:3,
即△AEF与△CDF的周长比为1:3;
(2)∵△AEF∽△CDF,
∴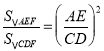 ,即
,即![]()
∴S△CDF=6×9=54 cm2;
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() cm2,
cm2,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
【题目】某数学兴趣小组根据学习函数的经验,对分段函数y=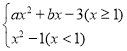 的图象与性质进了探究,请补充完整以下的探索过程.
的图象与性质进了探究,请补充完整以下的探索过程.
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 3 | 0 | ﹣1 | 0 | 1 | 0 | ﹣3 | … |
(1)填空:a= .b= .
(2)①提上述表格补全函数图象;②该函数图象是关于 对称的 (横线上填轴对称或中心对称)图形.
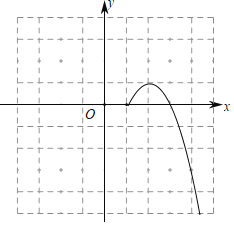
(3)若直线y=![]() x+t与该函数图象有三个交点,直接写出t的取值范围.
x+t与该函数图象有三个交点,直接写出t的取值范围.