题目内容
如图所示,已知正方形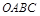 的面积为9 ,点
的面积为9 ,点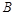 在函数
在函数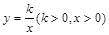 的图象上,点
的图象上,点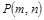 (
(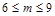 )是函数
)是函数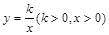 的图象上动点,过点
的图象上动点,过点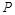 分别作
分别作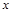 轴、
轴、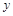 轴的垂线,垂足分别为
轴的垂线,垂足分别为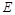 、
、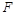 ,若设矩形
,若设矩形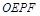 和正方形
和正方形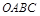 不重合的两部分的面积和为
不重合的两部分的面积和为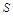 。
。
(1)求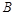 点坐标和
点坐标和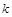 的值;(2)写出
的值;(2)写出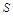 关于
关于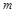 的函数关系和
的函数关系和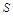 的最大值。
的最大值。
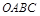 的面积为9 ,点
的面积为9 ,点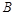 在函数
在函数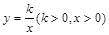 的图象上,点
的图象上,点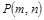 (
(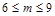 )是函数
)是函数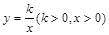 的图象上动点,过点
的图象上动点,过点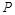 分别作
分别作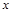 轴、
轴、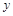 轴的垂线,垂足分别为
轴的垂线,垂足分别为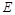 、
、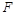 ,若设矩形
,若设矩形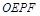 和正方形
和正方形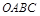 不重合的两部分的面积和为
不重合的两部分的面积和为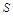 。
。
(1)求
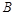 点坐标和
点坐标和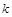 的值;(2)写出
的值;(2)写出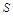 关于
关于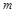 的函数关系和
的函数关系和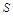 的最大值。
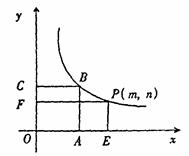
的最大值。(1)∵正方形OABC的面积为9,
∴正方形OABC的边长为3,即OA=3,AB=3,
∴B点坐标为(3,3).
又∵点B是函数 的图象上的一点,
的图象上的一点,
∴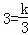 ,
,
∴k=9; 3分
(2)分两种情况:
若点P在点B的右侧,如图(1),
则PE=n,AE=m﹣3,
∴S=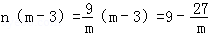 ;
;
若点P在点B的左侧,如图(2),
则PF=m,FC=n﹣3,
∴S=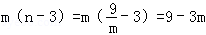 ;
;
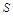 的最大值为9. 6分
的最大值为9. 6分
∴正方形OABC的边长为3,即OA=3,AB=3,
∴B点坐标为(3,3).
又∵点B是函数
 的图象上的一点,
的图象上的一点,∴
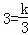 ,
,∴k=9; 3分
(2)分两种情况:
若点P在点B的右侧,如图(1),
则PE=n,AE=m﹣3,
∴S=
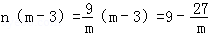 ;
;若点P在点B的左侧,如图(2),
则PF=m,FC=n﹣3,
∴S=
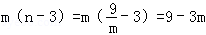 ;
;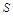 的最大值为9. 6分
的最大值为9. 6分(1)由于点B在函数y=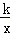 的图象上,而正方形OABC的面积为9,由此可以得到正方形边长为3,接着得到B的坐标及k的值;
的图象上,而正方形OABC的面积为9,由此可以得到正方形边长为3,接着得到B的坐标及k的值;
(2)分类讨论阴影部分(矩形)的面积。
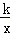 的图象上,而正方形OABC的面积为9,由此可以得到正方形边长为3,接着得到B的坐标及k的值;
的图象上,而正方形OABC的面积为9,由此可以得到正方形边长为3,接着得到B的坐标及k的值;(2)分类讨论阴影部分(矩形)的面积。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
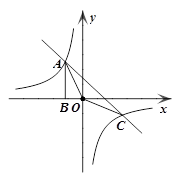
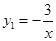 (x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0),当
(x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0),当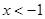 时,一次函数值大于反比例函数值,当
时,一次函数值大于反比例函数值,当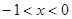 时,一次函数值小于反比例函数值.
时,一次函数值小于反比例函数值.
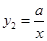 (x>0)的图象与
(x>0)的图象与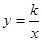 图象上一点,且矩形ABOC 的面积为3,则这个反比例函数解析式为 .
图象上一点,且矩形ABOC 的面积为3,则这个反比例函数解析式为 .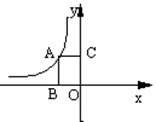
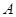 沿倾斜角为30°的山坡前进1500米到B,再次测得山顶D的仰角为60°,求山高CD. (结果保留根号)
沿倾斜角为30°的山坡前进1500米到B,再次测得山顶D的仰角为60°,求山高CD. (结果保留根号)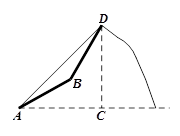
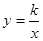 与直线
与直线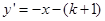 在第二象限的交点,AB⊥
在第二象限的交点,AB⊥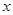 轴于B且S△ABO=
轴于B且S△ABO=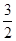 .
.
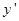 y.
y.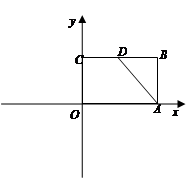
 上,则k的值为 ,直线OE与双曲线的另一个交点F的坐标是 ;
上,则k的值为 ,直线OE与双曲线的另一个交点F的坐标是 ;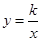 和一次函数
和一次函数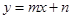 的图象交于A(-3,-1)、B(
的图象交于A(-3,-1)、B(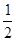 ,6)两点.分别求出反比例函数和一次函数的解析式.
,6)两点.分别求出反比例函数和一次函数的解析式.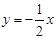 与双曲线
与双曲线 相交于A(-2,1)、B两点,则点B坐标为( )
相交于A(-2,1)、B两点,则点B坐标为( )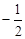 )
)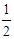 ,-1)
,-1)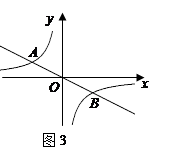
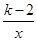 的图象位于第一、三象限,则k的取值范围是__________.
的图象位于第一、三象限,则k的取值范围是__________.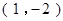 在反比例函数
在反比例函数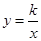 的图象上,则
的图象上,则 ____。
____。