题目内容
【题目】已知△ABC为等边三角形,E为射线BA上一点,D为直线BC上一点,ED=EC.
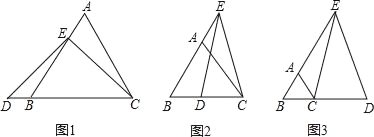
(1)当点E在AB的上,点D在CB的延长线上时(如图1),求证:AE+AC=CD;
(2)当点E在BA的延长线上,点D在BC上时(如图2),猜想AE、AC和CD的数量关系,并证明你的猜想;
(3)当点E在BA的延长线上,点D在BC的延长线上时(如图3),请直接写出AE、AC和CD的数量关系.
【答案】(1)证明见解析;(2)AC﹣AE=CD,证明见解析;(3)AE﹣AC=CD.
【解析】
(1)在CD上截取CF=AE,连接EF,运用“AAS”证明△EDB≌△ECF
得AE=BD,从而得证;
(2)在BC的延长线上截取CF=AE,连接EF,同理可得AE、AC和CD的数量关系;
(3)同(2)的探究过程可得AE、AC和CD的数量关系.
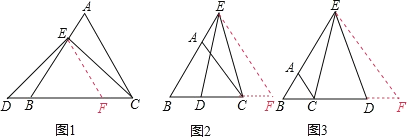
(1)证明:在CD上截取CF=AE,连接EF.
∵△ABC是等边三角形,
∴∠ABC=60°,AB=BC.
∴BF=BE,△BEF为等边三角形.
∴∠EBD=∠EFC=120°.
又∵ED=EC,
∴∠D=∠ECF.
∴△EDB≌△ECF (AAS)
∴CF=BD.
∴AE=BD.
∵CD=BC+BD,BC=AC,
∴AE+AC=CD;
(2)解:在BC的延长线上截取CF=AE,连接EF.
同(1)的证明过程可得AE=BD.
∵CD=BC﹣BD,BC=AC,
∴AC﹣AE=CD;
(3)解:AE﹣AC=CD.
(在BC的延长线上截取CF=AE,连接EF.证明过程类似(2)).
故答案为:(1)证明见解析;(2)AC﹣AE=CD,证明见解析;(3)AE﹣AC=CD.

练习册系列答案
相关题目



