题目内容
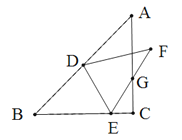
【题目】如图,△ABC中,∠ACB=90°,AB=2,BC=AC,D为AB的中点,E为BC上一点,将△BDE沿DE翻折,得到△FDE,EF交AC于点G,则△ECG的周长是___________.
【答案】![]()
【解析】
连接CE.根据“直角三角形斜边上的中线等于斜边的一半”、等腰三角形的性质以及折叠的性质推知EG+CG=EG+GF=EF=BE,
解:(1)如图,连接CD、CF.
∵Rt△ABC中,∠ACB=90°,AC=BC,D为AB边的中点,
∴BD=CD=1.BC=![]() ,
,
∵由翻折可知BD=DF,
∴CD=BD=DF=1,∠DFE=∠B=∠DCA=45°,
∴∠DCF=∠DFC,
∴∠DCF-∠DCA=∠DFC-∠DFE,即∠GCF=∠GFC,
∴GC=GF,
∴EG+CG=EG+GF=EF=BE,
∴△ECG的周长=EG+GC+CE=BE+EC=BC=![]() ,
,
故答案为:![]() .
.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
【题目】为了从甲、乙两名射击运动员中选拔一名参加比赛,对这两名运动员进行测试,他们10次射击命中的环数如下:
甲 | 7 | 9 | 8 | 6 | 10 | 7 | 9 | 8 | 6 | 10 |
乙 | 7 | 8 | 9 | 8 | 8 | 6 | 8 | 9 | 7 | 10 |
根据测试成绩,你认为选择哪一名运动员参赛更好?为什么?