Question

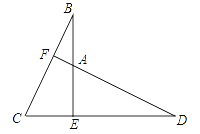
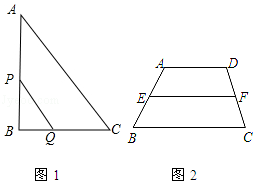
【题目】如图1，在△ABC中，AB=AC，点D是BC的中点，点E在AD上．

（1）求证：BE=CE；

（2）如图2，若BE的延长线交AC于点F，且BF⊥AC，垂足为F，∠BAC=45°，原题设其它条件不变．求证：△AEF≌△BCF．

Answer 1

【答案】（1）根据等腰三角形三线合一的性质可得∠BAE=∠EAC，然后利用“边角边”证明△ABE和△ACE全等，再根据全等三角形对应边相等证明即可。

（2）先判定△ABF为等腰直角三角形，再根据等腰直角三角形的两直角边相等可得AF=BF，再根据同角的余角相等求出∠EAF=∠CBF，然后利用“角边角”证明△AEF和△BCF全等即可。

【解析】

（1）根据等腰三角形三线合一的性质可得∠BAE=∠EAC，然后利用“边角边”证明△ABE和△ACE全等，再根据全等三角形对应边相等证明即可。

（2）先判定△ABF为等腰直角三角形，再根据等腰直角三角形的两直角边相等可得AF=BF，再根据同角的余角相等求出∠EAF=∠CBF，然后利用“角边角”证明△AEF和△BCF全等即可。

证明：（1）∵AB=AC，D是BC的中点，∴∠BAE=∠EAC。

在△ABE和△ACE中，∵，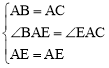

∴△ABE≌△ACE（SAS）。∴BE=CE。

（2）∵∠BAC=45°，BF⊥AF，∴△ABF为等腰直角三角形。∴AF=BF。

∵AB=AC，点D是BC的中点，∴AD⊥BC。∴∠EAF+∠C=90°。

∵BF⊥AC，∴∠CBF+∠C=90°。∴∠EAF=∠CBF。

在△AEF和△BCF中，∵，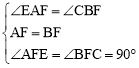

∴△AEF≌△BCF（ASA）。