题目内容
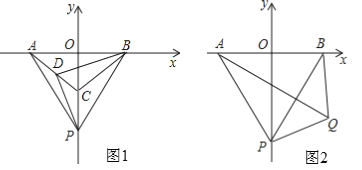
【题目】已知一个直角三角形纸片OAB,其中∠AOB=90°,OA=2,OB=4.如图,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边OB交于点C,与边AB交于点D.
(1)若折叠后使点B与点A重合,求点C的坐标.
(2)若折叠后点B落在边OA上的点为B′,是否存在点B′,使得四边形BCB′D是菱形?若存在,请说明理由并求出菱形的边长;若不存在,请说明理由.

【答案】(1)C(0,1.5);(2)存在点B',使得四边形BCB'D是菱形,此时菱形的边长为20﹣8![]() .
.
【解析】
(1)折叠后使点B与点A重合,则C在AB的中垂线上,Rt△AOC中利用勾股定理即可得到方程,求得C的坐标;
(2)当B'C∥AB(或B'D∥BO)时,四边形BCB'D是菱形,则△OB'C∽△OAB,依据相似三角形的对应边的比相等即可求得B′C的长度,然后根据△AB'D∽△AOB,即可求得B′D的长.从而证得B'C=BC=B'D=BD.
(1)设C(0,m),(m>0),
则CO=m,
BC=AC=(4﹣m),
在Rt△AOC中,有(4﹣m)2﹣m2=4,
整理得,12m=8,
∴m=1.5,
∴C(0,1.5);
(2)存在,当B'C∥AB(或B'D∥BO)时,四边形BCB'D是菱形,
∵∠AOB=90°,OA=2,OB=4,
∴AB=2![]() ,
,
∵B'C∥AB,
∴△OB'C∽△OAB,
∴![]() ,
,
设B'C=BC=x,则![]() ,
,
解得,x=2,
∵B'C∥AB,
∴∠CBD+∠BCB'=180°,
又∵∠CBD=∠CB'D,
∴∠CB'D+∠BCB'=180°,
∴B'D∥BO,
∴△AB'D∽△AOB,
∴![]() ,
,
设B'D=BD=y,
∴![]() ,
,
解得:y=20﹣8![]() ,
,
∴B'C=BC=B'D=BD,
∴四边形BCB'D是菱形,
∴存在点B',使得四边形BCB'D是菱形,此时菱形的边长为20﹣8![]() .
.

【题目】为了从甲、乙两名射击运动员中选拔一名参加比赛,对这两名运动员进行测试,他们10次射击命中的环数如下:
甲 | 7 | 9 | 8 | 6 | 10 | 7 | 9 | 8 | 6 | 10 |
乙 | 7 | 8 | 9 | 8 | 8 | 6 | 8 | 9 | 7 | 10 |
根据测试成绩,你认为选择哪一名运动员参赛更好?为什么?
【题目】某县为了了解初中生对安全知识掌握情况,抽取了50名初中生进行安全知识测试,并将测试成绩进行统计分析,绘制成了频数分布表和频数分布直方图(未完成). 安全知识测试成绩频数分布表
组别 | 成绩x(分数) | 组中值 | 频数(人数) |
1 | 90≤x<100 | 95 | 10 |
2 | 80≤x<90 | 85 | 25 |
3 | 70≤x<80 | 75 | 12 |
4 | 60≤x<70 | 65 | 3 |

(1)完成频数分布直方图;
(2)这个样本数据的中位数在第组;
(3)若将各组的组中值视为该组的平均成绩,则此次测试的平均成绩为;
(4)若将90分以上(含90分)定为“优秀”等级,则该县10000名初中生中,获“优秀”等级的学生约为人.
【题目】小明购买了一部新手机,到某通讯公司咨询移动电话资费情况,准备办理入网手续,该通讯公司工作人员向他介绍两种不同的资费方案:
方案代号 | 月租费(元) | 免费时间(分) | 超过免费时间的通话费(元/分) |
一 | 10 | 0 | 0.20 |
二 | 30 | 80 | 0.15 |
(1)分别写出方案一、二中,月话费(月租费与通话费的总和)y(单位:元)与通话时间x(单位:分)的函数关系式;
(2)画出(1)中两个函数的图象;
(3)若小明月通话时间为200分钟左右,他应该选择哪种资费方案最省钱.